题目内容
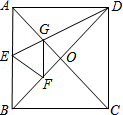
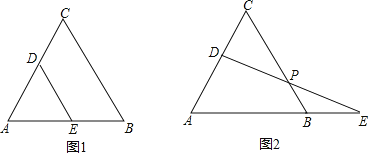
【题目】如图,D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)如图1,求证;AD=DE;
(2)如图2,DE交CB于点P.
①若DE⊥AC,PC=6,求BP的长;
②猜想PD与PE之间的数量关系,并证明你的结论.
【答案】(1)证明见解析;(2)①BP=3;②PD=PE,理由见解析.
【解析】
(1)只要证明△ADE是等边三角形即可;
(2)①利用直角三角形30度角性质即可解决问题;②过点D作DQ∥AB交BC于点Q,只要证明△CDQ是等边三角形,△DQP≌△EBP(AAS)即可解决问题.
(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵CD=BE,
∴AB-BE=AC-CD,即AD=AE,
∵∠A=60°,
∴△ADE是等边三角形.
∴AD=DE.

(2)①∵DE⊥AC,∠A=60°,
∴∠E=30°,
∵∠ABC=60°,
∴∠E=∠BPE=30°=∠CPD,
∴BP=BE,CD=![]() PC=3,
PC=3,
∵CD=BE,
∴BP=BE=3.
②PD=PE,理由如下:
如图2,过点D作DQ∥AB,交BC于点Q,
∴∠CDQ=∠A=60°,∠CQD=∠ABC=60°,∠DQP=∠EBP,
∴△DCQ是等边三角形,
∴DQ=CD=BE.
∵∠DPQ=∠EPB,∠DQP=∠EBP,
∴△DQP≌△EBP,
∴PD=PE.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目