题目内容
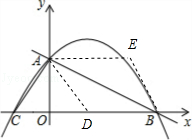
【题目】如图，在直角坐标系中，已知直线y=﹣ 
x+4与y轴交于A点，与x轴交于B点，C点的坐标为（﹣2，0）．
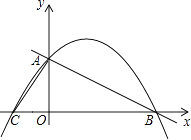
（1）求证：直线AB⊥AC；
（2）求经过A，B，C三点的抛物线l的解析式和对称轴；
（3）在直线AB上方的抛物线l上，是否存在一点P，使直线AB平分∠PBC？
若存在，请求出P点的坐标；若不存在，请说明理由．
【答案】
（1）
证明：当y=0时，x=8，即B（8，0），当x=0时，y=4，即A（0，4）．
∵△AOB、△AOC是直角三角形，
∴AC2=OC2+AO2=20，AB2=OB2+AO2=80，
∵AC2+AB2=20+80=100，BC2=[8﹣（﹣2）]2，
∴AC2+AB2=BC2，
∴AC⊥AB
（2）
解：设抛物线的解析式为y=ax2+bx+c，
将A、B、C点坐标代入，得
，
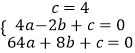解得a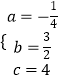 
，
抛物线的解析式为y=﹣ 
x2+ 
x+4，
y=﹣ x2+ x+4=﹣ （x﹣3）2+ 
，
抛物线的对称轴是x=3
（3）
解：在直线AB上方的抛物线l上，存在一点P，使直线AB平分∠PBC，理由如下：
如图ADBE是菱形，设D（x，0），BD=8﹣x，
由勾股定理，得
x2+42=（8﹣x）2，
解得x=3，
AD的解析式为y=﹣ 
x+4，
BE的解析式为y=﹣ x+b，将B点坐标代入，解得b= 
，
BE的解析式为y=﹣ x+ ，
联立BE与抛物线，得
，
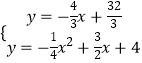消元化简，得
3x2﹣34x+80=0，
△=342﹣4×3×80=169，
∴x1=8（舍弃），x2= 
，
x= 时，y= 
∴当点P坐标为（ ， ）时，使直线AB平分∠PBC
【解析】（1）根据自变量与函数值的对应关系，可得A、B点坐标，根据勾股定理，可得AB、AC的长，根据勾股定理的逆定理，可得答案；（2）根据待定系数法，可得函数解析式；根据配方法，可得对称轴；（3）根据菱形的对角线平分一组对角，可得ADBE是菱形，根据平行间的一次项的系数相等，可得BE的解析式，根据解方程组，可得答案．
【考点精析】通过灵活运用勾股定理的概念，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．
