题目内容
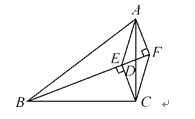
【题目】如图所示,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD,交BD的延长线于点F.
(1)试探索BE,BF和BD三者之间的数量关系,并加以证明;
(2)连接AE,CF,求证:AE∥CF.
【答案】(1) BE+BF=2BD,证明见解析;(2)证明见解析.
【解析】
(1)由已知条件易证△AFD≌△CED,由此可得DE=DF,这样结合BE=BD-DE,BF=BD+DF即可证得BE+BF=2BD;
(2)由(1)中所得△AFD≌△CED可得AD=CD,DE=DF,结合∠ADE=∠CDF即可证得△ADE≌△CDF,由此可得∠EAD=∠FCD,从而可得AE∥CF.
(1)BE+BF=2BD,理由如下:
∵BD为△ABC的中线,
∴AD=CD.
∵CE⊥BD于E,AF⊥BD于F,
∴∠F=∠CED=90°.
在△AFD和△CED中,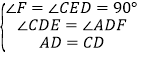 ,
,
∴△AFD≌△CED,
∴DE=DF.
∵BE+BF=(BD-DE)+(BD+DF),
∴BE+BF=2BD;
(2)∵△AFD≌△CED,
∴AD=CD,FD=ED,
又∵∠ADE=∠CDF.
∴△ADE≌△CDF,
∴∠EAD=∠FCD,
∴AE∥CF.

练习册系列答案
相关题目
【题目】某中学七年级四班的同学在体检中测量了自己的身高,并求出了该班同学的平均身高.
(1)下表给出了该班5名同学的身高情况(单位:cm),试完成该表,并求出该班同学的平均身高.
姓名 | 刘杰 | 刘涛 | 李明 | 张春 | 刘建 |
身高 | 161 |
|
| 165 | 155 |
身高与全班同 学平均身高差 | +3 | ﹣1 | 0 |
|
|
(2)谁最高?谁最矮?
(3)计算这5名同学的平均身高是多少?