ЬтФПФкШн
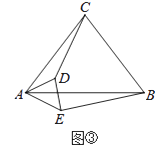
ЁОЬтФПЁПСтаЮABCDжаЁЂЁЯBADЃН120ЁуЃЌЕуOЮЊЩфЯпCA ЩЯЕФЖЏЕуЃЌзїЩфЯпOMгыжБЯпBCЯрНЛгкЕуEЃЌНЋЩфЯпOMШЦЕуOФцЪБеыа§зЊ60ЁуЃЌЕУЕНЩфЯпONЃЌЩфЯпONгыжБЯпCDЯрНЛгкЕуFЃЎ
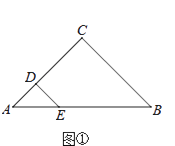
ЃЈ1ЃЉШчЭМЂйЃЌЕуOгыЕуAжиКЯЪБЃЌЕуEЃЌFЗжБ№дкЯпЖЮBCЃЌCDЩЯЃЌЧыжБНгаДГіCEЃЌCFЃЌCAШ§ЬѕЖЮЖЮжЎМфЕФЪ§СПЙиЯЕЃЛ
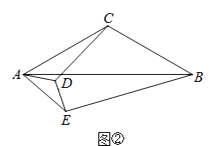
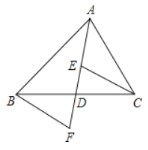
ЃЈ2ЃЉШчЭМЂкЃЌЕуOдкCAЕФбгГЄЯпЩЯЃЌЧвOAЃН![]() ACЃЌEЃЌFЗжБ№дкЯпЖЮBCЕФбгГЄЯпКЭЯпЖЮCDЕФбгГЄЯпЩЯЃЌЧыаДГіCEЃЌCFЃЌCAШ§ЬѕЯпЖЮжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ACЃЌEЃЌFЗжБ№дкЯпЖЮBCЕФбгГЄЯпКЭЯпЖЮCDЕФбгГЄЯпЩЯЃЌЧыаДГіCEЃЌCFЃЌCAШ§ЬѕЯпЖЮжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
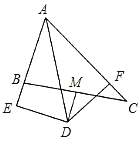
ЃЈ3ЃЉЕуOдкЯпЖЮACЩЯЃЌШєABЃН6ЃЌBOЃН2![]() ЃЌЕБCFЃН1ЪБЃЌЧыжБНгаДГіBEЕФГЄЃЎ
ЃЌЕБCFЃН1ЪБЃЌЧыжБНгаДГіBEЕФГЄЃЎ

ЁОД№АИЁПЃЈ1ЃЉCA=CE+CFЃЎЃЈ2ЃЉCF-CE=![]() ACЃЎЃЈ3ЃЉBEЕФжЕЮЊ3Лђ5Лђ1ЃЎ
ACЃЎЃЈ3ЃЉBEЕФжЕЮЊ3Лђ5Лђ1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМЂйжаЃЌНсТлЃКCA=CE+CFЃЎжЛвЊжЄУїЁїADFЁеЁїACEЃЈSASЃЉМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉНсТлЃКCF-CE=![]() ACЃЎШчЭМЂкжаЃЌШчЭМзїOGЁЮADНЛCFгкGЃЌдђЁїOGCЪЧЕШБпШ§НЧаЮЃЎжЛвЊжЄУїЁїFOGЁеЁїEOCЃЈASAЃЉМДПЩНтОіЮЪЬтЃЛ
ACЃЎШчЭМЂкжаЃЌШчЭМзїOGЁЮADНЛCFгкGЃЌдђЁїOGCЪЧЕШБпШ§НЧаЮЃЎжЛвЊжЄУїЁїFOGЁеЁїEOCЃЈASAЃЉМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЗжЫФжжЧщаЮЛГіЭМаЮЗжБ№ЧѓНтМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉШчЭМЂйжаЃЌНсТлЃКCA=CE+CFЃЎ
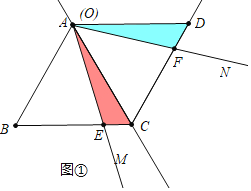
РэгЩЃКЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯBAD=120Ёу
ЁрAB=AD=DC=BCЃЌЁЯBAC=ЁЯDAC=60Ёу
ЁрЁїABCЃЌЁїACDЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁпЁЯDAC=ЁЯEAF=60ЁуЃЌ
ЁрЁЯDAF=ЁЯCAEЃЌ
ЁпCA=ADЃЌЁЯD=ЁЯACE=60ЁуЃЌ
ЁрЁїADFЁеЁїACEЃЈSASЃЉЃЌ
ЁрDF=CEЃЌ
ЁрCE+CF=CF+DF=CD=ACЃЌ
ЁрCA=CE+CFЃЎ
ЃЈ2ЃЉНсТлЃКCF-CE=![]() ACЃЎ
ACЃЎ
РэгЩЃКШчЭМЂкжаЃЌШчЭМзїOGЁЮADНЛCFгкGЃЌдђЁїOGCЪЧЕШБпШ§НЧаЮЃЎ

ЁпЁЯGOC=ЁЯFOE=60ЁуЃЌ
ЁрЁЯFOG=ЁЯEOCЃЌ
ЁпOG=OCЃЌЁЯOGF=ЁЯACE=120ЁуЃЌ
ЁрЁїFOGЁеЁїEOCЃЈASAЃЉЃЌ
ЁрCE=FGЃЌ
ЁпOC=OGЃЌCA=CDЃЌ
ЁрOA=DGЃЌ
ЁрCF-EC=CF-FG=CG=CD+DG=AC+![]() AC=
AC=![]() ACЃЌ
ACЃЌ
ЃЈ3ЃЉзїBHЁЭACгкHЃЎЁпAB=6ЃЌAH=CH=3ЃЌ
ЁрBH=3![]() ЃЌ
ЃЌ
ШчЭМЂл-1жаЃЌЕБЕуOдкЯпЖЮAHЩЯЃЌЕуFдкЯпЖЮCDЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ
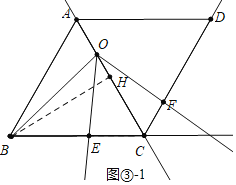
ЁпOB=2![]() ЃЌ
ЃЌ
ЁрOH=![]() =1ЃЌ
=1ЃЌ
ЁрOC=3+1=4ЃЌ
гЩЃЈ1ЃЉПЩжЊЃКCO=CE+CFЃЌ
ЁпOC=4ЃЌCF=1ЃЌ
ЁрCE=3ЃЌ
ЁрBE=6-3=3ЃЎ
ШчЭМЂл-2жаЃЌЕБЕуOдкЯпЖЮAHЩЯЃЌЕуFдкЯпЖЮDCЕФбгГЄЯпЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ
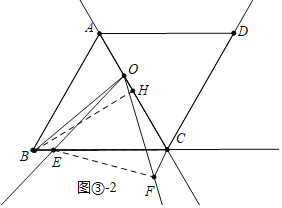
гЩЃЈ2ЃЉПЩжЊЃКCE-CF=OCЃЌ
ЁрCE=4+1=5ЃЌ
ЁрBE=1ЃЎ
ШчЭМЂл-3жаЃЌЕБЕуOдкЯпЖЮCHЩЯЃЌЕуFдкЯпЖЮCDЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ
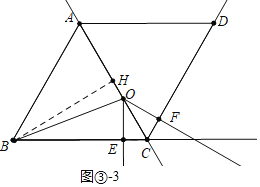
ЭЌЗЈПЩжЄЃКOC=CE+CFЃЌ
ЁпOC=CH-OH=3-1=2ЃЌCF=1ЃЌ
ЁрCE=1ЃЌ
ЁрBE=6-1=5ЃЎ
ШчЭМЂл-4жаЃЌЕБЕуOдкЯпЖЮCHЩЯЃЌЕуFдкЯпЖЮDCЕФбгГЄЯпЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ

ЭЌЗЈПЩжЊЃКCE-CF=OCЃЌ
ЁрCE=2+1=3ЃЌ
ЁрBE=3ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФBEЕФжЕЮЊ3Лђ5Лђ1ЃЎ

 аЁбЇПЮЪБзївЕШЋЭЈСЗАИЯЕСаД№АИ
аЁбЇПЮЪБзївЕШЋЭЈСЗАИЯЕСаД№АИ Н№АцПЮЬУПЮЪБбЕСЗЯЕСаД№АИ
Н№АцПЮЬУПЮЪБбЕСЗЯЕСаД№АИ ЕЅдЊШЋФмСЗПМОэЯЕСаД№АИ
ЕЅдЊШЋФмСЗПМОэЯЕСаД№АИ