题目内容
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.
小题1:求证:DE是⊙O的切线;
小题2:若DE=3,⊙O的半径为5,求BF的长.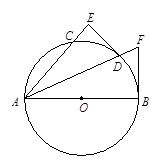
小题1:求证:DE是⊙O的切线;
小题2:若DE=3,⊙O的半径为5,求BF的长.
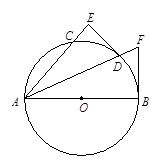
小题1:见解析
小题1:
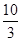
小题1:解:(1)连接OD.
∵AD平分∠BAC, ∴∠1=∠2.
又∵OA="OD" , ∴∠1=∠3.
∴∠2=∠3. ∴OD∥AE.
∵DE⊥AE ∴DE⊥OD.
而D在⊙O上, ∴DE是⊙O的切线.
小题1:过D作DG⊥AB 于G.
∵DE⊥AE ,∠1=∠2.
∴DG="DE=3" ,半径OD=5.
在Rt△ODG中,根据勾股定理:OG=4,
∴AG="AO+OG=5+4=9."
∵FB是⊙O的切线, AB是直径,
∴FB⊥AB.而DG⊥AB,
∴DG∥FB. △ADG∽△AFB, ∴易证BF=
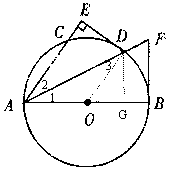

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
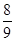 =0的两根,且O1O2=2,则⊙O1和⊙O2的位置关系是 ▲ .
=0的两根,且O1O2=2,则⊙O1和⊙O2的位置关系是 ▲ .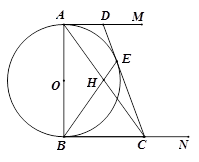
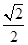 ,求 的值
,求 的值