��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD����ƽ���ı���ABDC
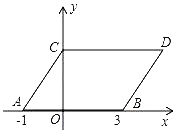
��1��ֱ��д����C��D�����ꣻ
��2������y���ϴ��ڵ� M������MA��MB��ʹS��MAB=Sƽ���ı���ABDC �� �����M�����꣮
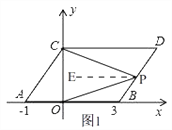
��3������P��ֱ��BD���˶�������PC��PO��
�뻭��ͼ�Σ�ֱ��д����CPO����DCP����BOP��������ϵ��
���𰸡���1��C��0��2����D��4��2����2����0��4����0����4����3���ٵ���P��BD�ϣ���CPO=��DCP+��BOP���ڵ���P���߶�BD���ӳ�����ʱ����CPO=��BOP����DCP���۵���P���߶�DB���ӳ�����ʱ����CPO=��DCP����BOP
��������������(1)�����ݵ��ƽ�Ʒ���ó���C�͵�D�����ꣻ(2)����M����Ϊ��0��m����Ȼ�����ƽ���ı��ε����ʵ���������������ȵó�m��ֵ���Ӷ��ó���M�����ꣻ(3)���ֵ���P��BD�ϡ�����P���߶�BD���ӳ�����ʱ�͵���P���߶�DB���ӳ�����ʱ��������ֱ�ͼ�Σ�Ȼ��ó��𰸣�
��⣺(1)���߽�A����1��0����B��3��0���ֱ�����ƽ��2����λ��������ƽ��1����λ��
��C��0��2����D��4��2����
(2)����AB=4��CO=2�� ��Sƽ���ı���ABDC=ABCO=4��2=8�� ��M����Ϊ��0��m����
�� ![]() ��4��|m|=8�����m=��4�� ��M���������0��4����0����4����
��4��|m|=8�����m=��4�� ��M���������0��4����0����4����
(3)���ٵ���P��BD�ϣ���ͼ1�� ��ƽ�Ƶ����ʵã�AB��CD��
����P��PE��AB����PE��CD�� ���DCP=��CPE����BOP=��OPE��
���CPO=��CPE+��OPE=��DCP+��BOP��
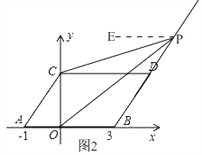
�ڵ���P���߶�BD���ӳ�����ʱ����ͼ2�� ��ƽ�Ƶ����ʵã�AB��CD��
����P��PE��AB����PE��CD�� ���DCP=��CPE����BOP=��OPE��
���CPO=��OPE����CPE=��BOP����DCP��
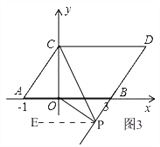
�۵���P���߶�DB���ӳ�����ʱ����ͼ3�� ͬ��2���ķ����ó���CPO=��DCP����BOP��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�