Question

已知等边三角形ABC和点P，设点P到△ABC的三边AB，AC，BC的距离为h₁，h₂，h₃，△ABC的高AM为h．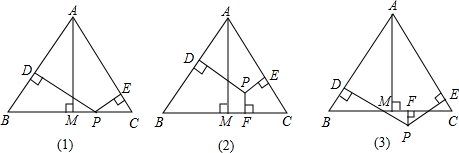
①当点P在△ABC的一边BC上．如图（1）所示，此时h₃=0，可得结论h₁+h₂+h₃______h．（填“＞”或“=”或“＜”）
②当点P在△ABC内部时，如图（2）所示；当P在△ABC外部时，如图（3）所示，这两种情况上述结论是否成立？若成立，给予证明；若不成立，写出新的关系式（不要求证明）．

Answer 1

①（1）h=h₁+h₂，理由如下：
连接AP，则S_△ABC=S_△ABP+S_△APC
∴

1

2

BC•AM=

1

2

AB•PD+

1

2

AC•PF
即

1

2

BC•h=

1

2

AB•h₁+

1

2

AC•h₂
又∵△ABC是等边三角形
∴BC=AB=AC，
∴h=h₁+h₂．


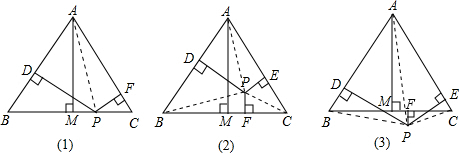
②当点P在△ABC内时，结论成立．证明如下：
如图2，连接PA，PB，PC
∵S_△PAB+S_△PAC+S_△PBC=S_△ABC
∴

1

2

AB•h1+

1

2

AC•h2+

1

2

BC•h3=

1

2

BC•h
∵△ABC是等边三角形
∴AB=AC=BC，
∴h₁+h₂+h₃=h
当点P在△ABC外时，结论不成立，
理由如下：如图（3）连接PB，PC，PA
由三角形的面积公式得：S_△ABC=S_△PAB+S_△PAC-S_△PBC，
即

1

2

BC•AM=

1

2

AB•PD+

1

2

AC•PE-

1

2

BC•PF，
∵AB=BC=AC，
∴h₁+h₂-h₃=h．