题目内容
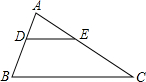
 如图,DE∥BC,∠D=2∠DBC,∠1=∠2,则∠DEB的度数为
如图,DE∥BC,∠D=2∠DBC,∠1=∠2,则∠DEB的度数为
- A.30°
- B.45°
- C.60°
- D.无法计算
A
分析:本题考查的是平行线的性质.由两直线平行,同旁内角互补可得∠D+∠DBC=180°,然后结合已知条件求出∠1后,易求∠DEB.
解答:∵DE∥BC,∴∠D+∠DBC=180°;
又∵∠D=2∠DBC,∴∠D=120°,∠DBC=60°;
∵∠1=∠2,∴∠1=∠2=30°,
∴∠2=∠DEB=30°(两直线平行,内错角相等).
故选A.
点评:本题主要是考查两直线平行,内错角相等,同旁内角互补的平行线性质.
分析:本题考查的是平行线的性质.由两直线平行,同旁内角互补可得∠D+∠DBC=180°,然后结合已知条件求出∠1后,易求∠DEB.
解答:∵DE∥BC,∴∠D+∠DBC=180°;
又∵∠D=2∠DBC,∴∠D=120°,∠DBC=60°;
∵∠1=∠2,∴∠1=∠2=30°,
∴∠2=∠DEB=30°(两直线平行,内错角相等).
故选A.
点评:本题主要是考查两直线平行,内错角相等,同旁内角互补的平行线性质.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为
如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为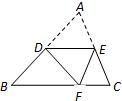 12、如图,DE∥BC,将△ABC沿DE所在的直线折叠,点A正好落在BC边上F处,若∠B=40°,则∠BDF=
12、如图,DE∥BC,将△ABC沿DE所在的直线折叠,点A正好落在BC边上F处,若∠B=40°,则∠BDF=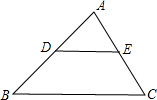 如图,DE∥BC,AD:DB=3:4,则△ADE与△ABC的周长之比为
如图,DE∥BC,AD:DB=3:4,则△ADE与△ABC的周长之比为 (1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( )
(1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( )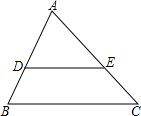 (1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.
(1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.