Question

【题目】如图，△ABC中，∠C=90°．

（1）在BC边上作一点P，使得点P到点C的距离与点P到边AB的距离相等（尺规作图，不写作法，保留作图痕迹）；
（2）在（1）的条件下，若AC=8，BC=6，求CP的长．

Answer 1

【答案】
（1）解：如图，点P即为所求

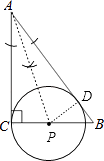
（2）解：作PD⊥AB于点，如图，

∵AP平分∠CAB，PD⊥AB于D，∠C=90°，

∴PD=PC．

在Rt△ADP和Rt△ACP中

，

∴Rt△ADP≌Rt△ACP（HL），

∴AD=AC=8，

在Rt△ABC中，AB= =10，

∴BD=10﹣8=2，

设PC=x，则PD=x，BP=6﹣x，

在Rt△BDP中，∵PD2+BD2=PB2，

∴（6﹣x）2=x2+22，解得x= ．

答：CP的长为

【解析】（1）根据角平分线的性质作图，作∠BAC的平分线交BC于P点，则点P到点C的距离与点P到边AB的距离相等。
（2）添加辅助线，过点点P作PD⊥AB于点D，根据角平分线性质得PD=PC，则可证明Rt△ADP≌Rt△ACP得到AD=AC=8，再利用勾股定理计算出AB=10，则BD=2，设PC=x，则PD=x，BP=6-x，在Rt△BDP中，利于勾股定理得建立方程，然后解方程即可。

【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识，掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．