题目内容
如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.
①求弧BO的度数;
②求⊙C的半径;
③求过点B、M、O的二次函数解析式.
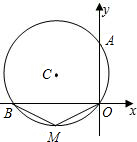
①求弧BO的度数;
②求⊙C的半径;
③求过点B、M、O的二次函数解析式.

(1)连接AB,AM,则由∠AOB=90°,故AB是直径,
由∠BAM+∠OAM=∠BOM+∠OBM=180°-120°=60°,
得∠BAO=60°,∴弧BO的度数为120°;
(2)又AO=6,故cos∠BAO=
,AB=
=12,
从而⊙C的半径为6.
(3)由(1)得,BO=
=6
,
过C作CE⊥OA于E,CF⊥OB于F,
则EC=OF=
BO=
×6
=3
,CF=OE=
OA=3.
故C点坐标为(-3
,3).点B(-6
,0),点M(-3
,-3),
设过点B、M、O的二次函数解析式为:y=ax2+bx,把点B(-6
,0),点M(-3
,-3)代入,
解得:a=
,b=
,
故二次函数解析式为:y=
x2+
x.
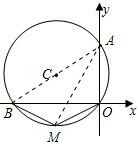
由∠BAM+∠OAM=∠BOM+∠OBM=180°-120°=60°,
得∠BAO=60°,∴弧BO的度数为120°;
(2)又AO=6,故cos∠BAO=
| AO |
| AB |
| 6 |
| cos60° |
从而⊙C的半径为6.
(3)由(1)得,BO=
| 122-62 |
| 3 |
过C作CE⊥OA于E,CF⊥OB于F,
则EC=OF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
故C点坐标为(-3
| 3 |
| 3 |
| 3 |
设过点B、M、O的二次函数解析式为:y=ax2+bx,把点B(-6
| 3 |
| 3 |
解得:a=
| 1 |
| 9 |
2
| ||
| 3 |
故二次函数解析式为:y=
| 1 |
| 9 |
2
| ||
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

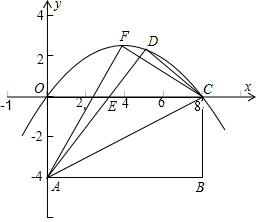
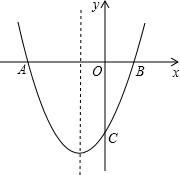
 为A(-1,0),C(0,-3).
为A(-1,0),C(0,-3).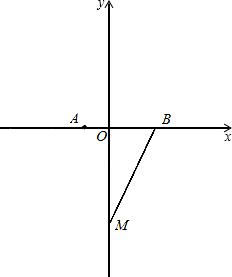 点M在y轴的负半轴上,且|AB|=6,cos∠OBM=
点M在y轴的负半轴上,且|AB|=6,cos∠OBM=