题目内容
阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d= .
.

例:求点P(1,2)到直线y=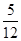 x-
x-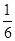 的距离d时,先将y=
的距离d时,先将y=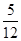 x-
x-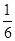 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=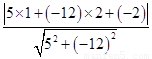 =
= .
.
解答下列问题:
如图2,已知直线y=-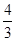 x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).

(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
【答案】
(1) 6 (2)存在,P(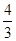 ,
,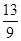 ),△PAB面积的最小值为
),△PAB面积的最小值为 ×5×
×5×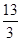 =
=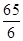
【解析】
试题分析:(1)将y=-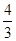 x-4化为4x+3y+12=0,由上述距离公式得:
x-4化为4x+3y+12=0,由上述距离公式得:
d=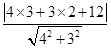 =6
=6
∴点M到直线AB的距离为6
(2)存在
设P(x,x2-4x+5),则点P到直线AB的距离为:
d=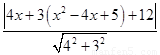
由图象知,点P到直线AB的距离最小时x>0,x2-4x+5>0
∴d=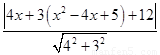 =
=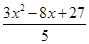 =
=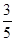 (x-
(x-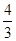 )2+
)2+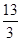
∴当x=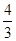 时,d最小,为
时,d最小,为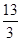
当x=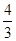 时,x2-4x+5=(
时,x2-4x+5=(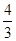 )2-4×
)2-4×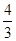 +5=
+5=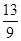 ,∴P(
,∴P(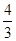 ,
,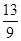 )
)
在y=-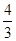 x-4中,令x=0,则y=-4,∴B(0,-4)
x-4中,令x=0,则y=-4,∴B(0,-4)
令y=0,则xy=-3。∴A(-3,0)
∴AB=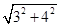 =5
=5
∴△PAB面积的最小值为 ×5×
×5×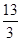 =
=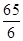
考点:直线与抛物线
点评:本题考查直线与抛物线,掌握直线与抛物线的性质,会求点到直线的距离

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 28、
28、 阅读下列材料:
阅读下列材料: