Question

【题目】如图，已知△ABC中，四边形DEGF为正方形，D、E在线段AC、BC上，F、G在AB上，如果S△ADF=S△CDE=1，S△BEG=3，求△ABC的面积．

Answer 1

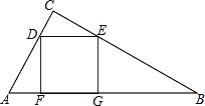
【答案】S△ABC=9．

【解析】

过C作CH⊥AB于H，交DE于M，设AF=a，正方形DFGE的边长为b，CM=h，由于S△CDE=bh=1，S△AFD=ab=1，于是得到a=h，CH=h+b=a+b，根据S△BEG=BGb=3，得到GB=3a，于是求出S△ABC=ABCH=（a+b+3a）（a+b）=b2+5，由于ab=2，于是求得2a2+b2=b2，通过化简即可得到结论．

解：过C作CH⊥AB于H，交DE于M，

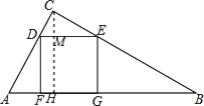
设AF=a，正方形DFGE的边长为b，CM=h，

∴S△CDE= bh=1，S△AFD= ab=1，

∴a=h，

∴CH=h+b=a+b，

∵S△BEG= BGb=3，

∴GB=3a，

∴S△ABC= ABCH= （a+b+3a）（a+b）=b2+5，

∵ab=2，

∴2a2+ b2=b2，

∴b=2a，

∴ b×b=2，

∴b2=4，

∴S△ABC=b2+5=9．