题目内容
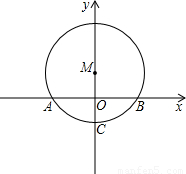 如图,在⊙M中,弧AB所对的圆心角为120°,已知⊙M的半径为2cm,并建立如图所示的直角坐标系.
如图,在⊙M中,弧AB所对的圆心角为120°,已知⊙M的半径为2cm,并建立如图所示的直角坐标系.(1)求圆心M的坐标;
(2)求经过A,B,C三点的抛物线的解析式;
(3)点D是弦AB所对的优弧上一动点,求四边形ACBD的最大面积.
【答案】分析:(1)连接MA,MB,根据等腰三角形的性质可知∠AMO= AMB=60°,由直角三角形的性质可求出M点的坐标.
AMB=60°,由直角三角形的性质可求出M点的坐标.
(2)根据△AOM与△BOM是直角三角形,∠AMO=∠BMO=60°,可求出A、B两点的坐标,因为A、B两点关于y轴对称,故此抛物线关于y轴对称,根据此特点可设出抛物线的解析式,把A、B两点的坐标代入即可求出未知数的值,从而求出其解析式.
(3)因为四边形ACBD的面积等于△ABC与△ABD的面积之和,而△ABC的面积为定值,△ABD的底边长为定值,故当△ABD的高最长时四边形的面积最大.根据直径是最长的弦可知当D在y轴上时△ABD的高最长.根据三角形的面积公式及圆的半径长可计算出四边形的面积.
解答: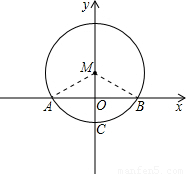 解:(1)连MA,MB,
解:(1)连MA,MB,
∵MA=MB OM⊥AB∠AMB=120°
∴∠BMO= ∠AMB=60°
∠AMB=60°
∴∠OBM=30° 2分
∴OM= MB=1 1分
MB=1 1分
∴M(0,1)1分
(2)∵OC=MC-MO=1 OB=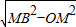 =
=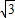
∴C(0,-1)B( ,O) 2分
,O) 2分
∵经过A,B,C三点的抛物线关于y轴对称
∴设经过A,B,C三点的抛物线的解析式为y=ax2+c 1分
把C(0,-1)和(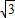 ,0)分别代入上式
,0)分别代入上式
得:a= ,c=-1 1分
,c=-1 1分
∴y= x2-1. 1分
x2-1. 1分
(3)∵S四边形ACBD=S△ABC+S△ABD,又S△ABC与AB均为定值1分
∴当△ABD边上的高最大时,S△ABD最大,
此时点D为⊙M与y轴交点,由于⊙M的半径为2cm,OM=1cm
∴OD=3cm,
此时S四边形ACBD=S△ABC+S△ABD= ×2
×2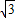 ×1+
×1+ ×2
×2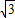 ×3=
×3=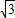 +3
+3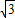 =4
=4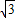 cm2.
cm2.
点评:本题考查的是圆的性质及二次函数图象上点的坐标特点,比较复杂,但难度适中.
 AMB=60°,由直角三角形的性质可求出M点的坐标.
AMB=60°,由直角三角形的性质可求出M点的坐标.(2)根据△AOM与△BOM是直角三角形,∠AMO=∠BMO=60°,可求出A、B两点的坐标,因为A、B两点关于y轴对称,故此抛物线关于y轴对称,根据此特点可设出抛物线的解析式,把A、B两点的坐标代入即可求出未知数的值,从而求出其解析式.
(3)因为四边形ACBD的面积等于△ABC与△ABD的面积之和,而△ABC的面积为定值,△ABD的底边长为定值,故当△ABD的高最长时四边形的面积最大.根据直径是最长的弦可知当D在y轴上时△ABD的高最长.根据三角形的面积公式及圆的半径长可计算出四边形的面积.
解答:
 解:(1)连MA,MB,
解:(1)连MA,MB,∵MA=MB OM⊥AB∠AMB=120°
∴∠BMO=
 ∠AMB=60°
∠AMB=60°∴∠OBM=30° 2分
∴OM=
 MB=1 1分
MB=1 1分∴M(0,1)1分
(2)∵OC=MC-MO=1 OB=
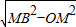 =
=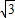
∴C(0,-1)B(
 ,O) 2分
,O) 2分∵经过A,B,C三点的抛物线关于y轴对称
∴设经过A,B,C三点的抛物线的解析式为y=ax2+c 1分
把C(0,-1)和(
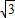 ,0)分别代入上式
,0)分别代入上式得:a=
 ,c=-1 1分
,c=-1 1分∴y=
 x2-1. 1分
x2-1. 1分(3)∵S四边形ACBD=S△ABC+S△ABD,又S△ABC与AB均为定值1分
∴当△ABD边上的高最大时,S△ABD最大,
此时点D为⊙M与y轴交点,由于⊙M的半径为2cm,OM=1cm
∴OD=3cm,
此时S四边形ACBD=S△ABC+S△ABD=
 ×2
×2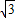 ×1+
×1+ ×2
×2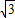 ×3=
×3=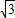 +3
+3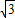 =4
=4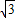 cm2.
cm2.点评:本题考查的是圆的性质及二次函数图象上点的坐标特点,比较复杂,但难度适中.

练习册系列答案
相关题目
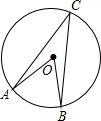 如图,在⊙O中,弧AB=50°,则圆周角∠ACB的大小为( )
如图,在⊙O中,弧AB=50°,则圆周角∠ACB的大小为( )| A、25° | B、50° | C、100° | D、130° |
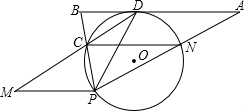 作PM∥AB交DC的延长线于M,
作PM∥AB交DC的延长线于M, 如图,在⊙M中,弧AB所对的圆心角为120°,已知⊙M的半径为2cm,并建立如图所示的直角坐标系.
如图,在⊙M中,弧AB所对的圆心角为120°,已知⊙M的半径为2cm,并建立如图所示的直角坐标系. 如图,在⊙O中,弧AB=60°,AB=6,
如图,在⊙O中,弧AB=60°,AB=6,