题目内容
如图，在⊙O中，弧DC=弧DN，点P为⊙O上一点，过D作CN的平行线交PN，PC的延长线于A，B，过P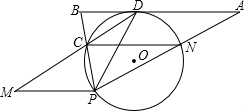
作PM∥AB交DC的延长线于M，（1）求证：AB为⊙O的切线；
（2）若PN=3AN的值，求
| PD | DM |
分析：（1）连接OD，由弧DC=弧DN，则知OD⊥CN，又知到AB∥CN，故能证明OD⊥AB，
（2）连接DN，先证△DCP∽△DPM，得到
=
，再证△ADN∽△APD，得到AD=2AN，最后得到
的值．
（2）连接DN，先证△DCP∽△DPM，得到
| PD |
| DM |
| CD |
| PD |
| PD |
| DM |
解答：（1）证明：连接OD，
∵弧DC=弧DN，
∴OD⊥CN，
∵AB∥CN，
∴OD⊥AB，
∴AB为⊙O切线．
（2）解：连接DN，
∵
=
，
∴∠DCN=∠CPD，
又PM∥AB，CN∥AB，
∴CN∥MP，
∴∠DCN=∠M，
∴∠DPC=∠M，又∠CDP=∠PDM，
∴△DCP∽△DPM，
∴
=
，
∵∠DAN=∠PAD，∠ADN=∠APD，
∴△ADN∽△APD，得到AD=2AN，
又
=
=
=
，
即
=
．
∵弧DC=弧DN，
∴OD⊥CN，
∵AB∥CN，
∴OD⊥AB，
∴AB为⊙O切线．
（2）解：连接DN，
∵
 |
| DC |
|
| DN |
∴∠DCN=∠CPD，
又PM∥AB，CN∥AB，
∴CN∥MP，
∴∠DCN=∠M，
∴∠DPC=∠M，又∠CDP=∠PDM，
∴△DCP∽△DPM，
∴
| PD |
| DM |
| CD |
| PD |
∵∠DAN=∠PAD，∠ADN=∠APD，
∴△ADN∽△APD，得到AD=2AN，
又
| AN |
| AD |
| DN |
| PD |
| CD |
| PD |
| 1 |
| 2 |
即
| PD |
| DM |
| 1 |
| 2 |
点评：本题考查了切线的判定，相似三角形的判定等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．
练习册系列答案
相关题目
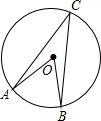如图，在⊙O中，弧AB=50°，则圆周角∠ACB的大小为（ ）| A、25° | B、50° | C、100° | D、130° |
如图，在⊙M中，弧AB所对的圆心角为120°，已知⊙M的半径为2cm，并建立如图所示的直角坐标系．
如图，在⊙O中，弧AB=60°，AB=6，