Question

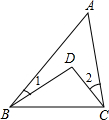
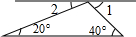
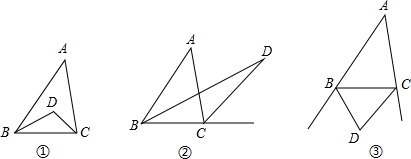
如图①，△ABC中，DC，BD分别是∠ACB和∠ABC的平分线，且∠A=α
（1）用含α的代数识别是∠CDB；
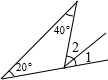
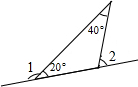
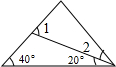
（2）若把图①中∠ACB的平分线DC改为∠ACB的外角的平分线（如图②），怎样用含α的代数式别是∠CDB．
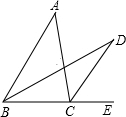
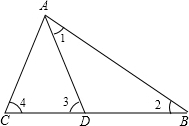
（3）若把图①中“DC，DB分别是∠ACB和∠ABC的平分线”改成“DC，BD分别是∠ACB和∠ABC的外角的平分线”，（如图③），怎样用含α的代数式别是∠CDB．

Answer 1

（1）∵∠A=α，∴∠ABC+∠ACB=180°-α，
∵DC，BD分别是∠ACB和∠ABC的平分线，
∴∠DBC+∠DCB=

1

2

×（∠ABC+∠ACB）=90°-α，
∴∠CDB=180°-（∠DBC+∠DCB）=90°+

α

2

；

（2）设BC的延长线上有一点E．
∵∠DCE是△BCD的一个外角，
∴∠D=∠DCE-∠DBC，
同理：∠A=∠ACE-∠ABC，
∵CD和BD分别为角平分线，
∴∠DCE=

1

2

∠ACE，∠DBC=

1

2

∠ABC，
∴∠CDB=

α

2

；

（3）∵∠A=α，
∴∠ABC+∠ACB=180°-α，
∵DC，BD分别是∠ACB和∠ABC的外角的平分线，
∴∠DBC+∠DCB=

1

2

×[360°-（∠ABC+∠ACB）]=90°+

α

2

，
∴∠CDB=CDB=180°-（∠DBC+∠DCB）=90°-

α

2

．