题目内容
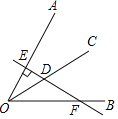
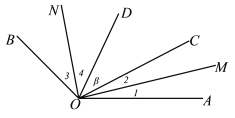
【题目】如图，射线OC、OD在∠AOB内部，∠AOB＝
，∠COD＝
，分别作∠AOC和∠BOD的平分线OM、ON，
（1）当＝130°，＝40°时，请你填空：∠1＋∠3＝______°，∠MON＝______°；
（2）聪明的小芳通过探究发现，当射线OC、OD的位置在∠AOB内变化时，∠MON与、之间总满足∠MON＝
，你是否认同她的这一结论？请说明理由；
【答案】（1）45°；85°；（2）是，理由见解析
【解析】
（1）先求出∠BOD＋∠AOC，然后根据角平分线的定义可得∠3=∠4=
∠BOD，∠1=∠2=∠AOC，从而求出∠1＋∠3和∠2＋∠4，即可求出∠MON；
（2）先求出∠BOD＋∠AOC，然后根据角平分线的定义可得∠4=∠BOD，∠2=∠AOC，从而求出∠2＋∠4，即可求出∠MON；
解：（1）∵∠AOB＝
=130°，∠COD＝
=40°
∴∠BOD＋∠AOC=∠AOB－∠COD=90°
∵ON、OM分别平分∠BOD和∠AOC
∴∠3=∠4=∠BOD，∠1=∠2=∠AOC
∴∠1＋∠3＝∠2＋∠4=∠AOC ＋∠BOD
=（∠AOC ＋∠BOD）
=×90°
=45°
∴∠MON＝∠2＋∠4＋∠COD
=45°＋40°
=85°
故答案为：45°；85°；
（2）是，理由如下：
∵∠AOB＝，∠COD＝
∴∠BOD＋∠AOC=∠AOB－∠COD=－
∵ON、OM分别平分∠BOD和∠AOC
∴∠4=∠BOD，∠2=∠AOC
∴∠2＋∠4=∠AOC ＋∠BOD
=（∠AOC ＋∠BOD）
=
∴∠MON＝∠2＋∠4＋∠COD
=＋
=
练习册系列答案
相关题目
