题目内容
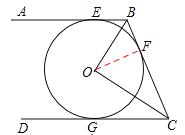
【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.

【答案】(1)证明见解析;(2)6.4cm.
【解析】
试题分析:(1)由AB∥CD得出∠ABC+∠BCD=180°,根据切线长定理得出OB、OC平分∠EBF和∠BCG,也就得出了∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°.从而证得∠BOC是个直角,从而得出BO⊥CO;
(2)根据勾股定理求得AB=10cm,根据RT△BOF∽RT△BCO得出BF=3.6cm,根据切线长定理得出BE=BF=3.6cm,CG=CF,从而求得BE和CG的长.
试题解析:解:(1)证明:∵AB∥CD,∴∠ABC+∠BCD=180°.
∵AB、BC、CD分别与⊙O相切于E、F、G,∴BO平分∠ABC,CO平分∠DCB.
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠DCB.
∠DCB.
∴∠OBC+∠OCB=![]() (∠ABC+∠DCB)=
(∠ABC+∠DCB)=![]() ×180°=90°.
×180°=90°.
∴∠BOC=90°. ∴BO⊥CO.
(2)如答图,连接OF,则OF⊥BC,
∴Rt△BOF∽Rt△BCO. ∴![]() .
.
∵在RT△BOF中,BO=6cm,CO=8cm,
∴根据勾股定理得,BC=10cm,
∴![]() . ∴BF=3.6cm,
. ∴BF=3.6cm,
∵AB、BC、CD分别与⊙O相切,∴BE=BF=3.6cm,CG=CF.
∵CF=BC﹣BF=10﹣3.6=6.4cm,∴CG=CF=6.4cm.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


