题目内容
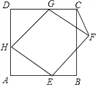
【题目】已知，如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD边AB，CD，DA上，AH=2，连接CF．
（1）当DG=2时，求△FCG的面积；
（2）设DG=x，用含x的代数式表示△FCG的面积；
（3）判断△FCG的面积能否等于1，并说明理由．
【答案】(1)4;(2)6-x;(3)见解析.
【解析】分析：(1)要求△FCG的面积,可以转化到面积易求的三角形中,通过证明△DGH≌△CFG得出.(2)欲求△FCG的面积,由已知得CG的长易求,只需求出GC边的高,通过证明△AHE≌△MFG可得;
(3)若
,由
,得x=5,此时,在△DGFH中,HG=
.相应地,在△AHE中,AE=
>6,即点E已经不在边AB上.故不可能有.
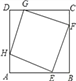
详解：（1）∵正方形ABCD中，AH=2，
∴DH=4，
∵DG=2，
∴HG=2
，即菱形EFGH的边长为2．
在△AHE和△DGH中，
∵∠A=∠D=90°，AH=DG=2，EH=HG=2，
∴△AHE≌△DGH（HL），
∴∠AHE=∠DGH，
∵∠DGH+∠DHG=90°，
∴∠DHG+∠AHE=90°，
∴∠GHE=90°，即菱形EFGH是正方形，
同理可以证明△DGH≌△CFG，
∴∠FCG=90°，即点F在BC边上，同时可得CF=2，
从而S△FCG=
×4×2=4．
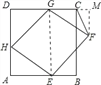
（2）作FM⊥DC，M为垂足，连接GE，
∵AB∥CD，
∴∠AEG=∠MGE，
∵HE∥GF，
∴∠HEG=∠FGE，
∴∠AEH=∠MGF．
在△AHE和△MFG中，
∴△AHE≌△MFG（AAS），
∴FM=HA=2，
即无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2．
因此S△FCG=
×2×（6﹣x）=6﹣x．
（3）若S△FCG=1，由（2）知S△FCG=6﹣x，得x=5，
∴在△DGH中，HG=
，
∴在△AHE中，AE=
，即点E已经不在边AB上．
∴不可能有S△FCG=1．
另法：∵点G在边DC上，
∴菱形的边长至少为DH=4，
当菱形的边长为4时：
∵点E在AB边上且满足AE=2
，此时，当点E逐渐向右运动至点B时，HE的长（即菱形的边长）将逐渐变大，
∴最大值为HE=2
．
此时，DG=2
，故0≤x≤2．
∵函数S△FCG=6﹣x的值随着x的增大而减小，
∴当x=2时，S△FCG取得最小值为6﹣2．
又∵6﹣2
=1，
∴△FCG的面积不可能等于1．
