题目内容
【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
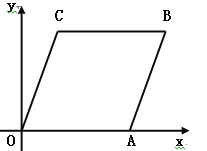
【答案】(1)点C的坐标为(2,6);
(2)点D的坐标是(![]() ,0)
,0)
(3)α﹣β=θ,理由见解析.
【解析】分析:(1)由点的坐标的特点,确定出FC=2,OF=6得出C(2,6) ;
(2)分点D在线段OA和在OA延长线两种情况进行计算;
(3)分点D在线段OA上时, ![]() 和在OA延长线
和在OA延长线![]() 两种情况进行计算;
两种情况进行计算;
解:(1)C(2,6);
(2)设D(x,0),当△ODC的面积是△ABD的面积的3倍时,
若点D在线段OA上,
∵OD=3AD,
∴![]() ×6x=3×
×6x=3×![]() ×6(6﹣x),
×6(6﹣x),
∴x=![]() ,
,
∴D(![]() ,0);
,0);
若点D在线段OA延长线上,
∵OD=3AD,
∴![]() ×6x=3×
×6x=3×![]() ×6(x﹣6),
×6(x﹣6),
∴x=9,
∴D(9,0)
(3)如图2.
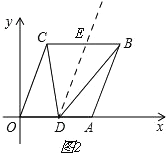
过点D作DE∥OC,
由平移的性质知OC∥AB.
∴OC∥AB∥DE.
∴∠OCD=∠CDE,∠EDB=∠DBA.
若点D在线段OA上,
∠CDB=∠CDE+∠EDB=∠OCD+∠DBA,
即α+β=θ;
若点D在线段OA延长线上,
∠CDB=∠CDE﹣∠EDB=∠OCD﹣∠DBA,
即α﹣β=θ.

练习册系列答案
相关题目