题目内容
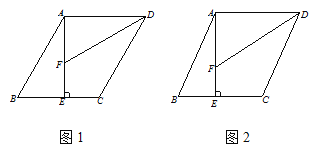
【题目】如图,已知![]() ,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.
,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.

解:BE ______ CF.
理由是:![]() 已知
已知![]() .
.
![]() ______
______ ![]() ______
______ ![]() 垂直的定义
垂直的定义![]()
![]() 已知
已知![]() .
.
![]() =______
=______ ![]() .(等式的基本性质)
.(等式的基本性质)
即![]() ______
______
![]() ______
______ ![]() ( ______________________
( ______________________ ![]()
【答案】∥;ABC;BCD;∠BCD;∠BCF;∥;内错角相等,两直线平行
【解析】分析:先根据垂直的定义得出∠ABC=∠BCD=90°,再根据∠1=∠2可得出∠EBC=∠BCF,进而可得出结论.
详解:BE∥CF.
理由:∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=∠BCD=90°(垂直的定义).
∵∠1=∠2(已知),
∴∠ABC∠1=∠BCD∠2,即∠EBC=∠BCF,
∴BE∥CF(内错角相等,两直线平行).
故答案为:∥;ABC,BCD;=∠BCD;∠BCF;∥,内错角相等,两直线平行

练习册系列答案
相关题目
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?