题目内容
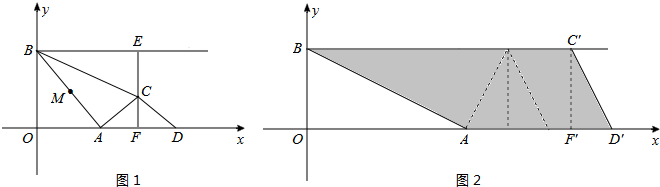
(2013•丽水)如图1,点A是x轴正半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连结AC,BC,CD,设点A的横坐标为t.
(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段BD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到△C′D′F′,再将A,B,C′,D′为顶点的四边形沿C′F′剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的点C′的坐标.
(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段BD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到△C′D′F′,再将A,B,C′,D′为顶点的四边形沿C′F′剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的点C′的坐标.

分析:(1)由Rt△ACF∽Rt△BAO,得CF=
OA=
t,由此求出CF的值;
(2)①由Rt△ACF∽Rt△BAO,可以求得AF的长度;若点C落在线段BD上,则有△DCF∽△DBO,根据相似比例式列方程求出t的值;
②有两种情况,需要分类讨论:当0<t≤8时,如题图1所示;当t>8时,如答图1所示.
(3)本问涉及图形的剪拼.在△CDF沿x轴左右平移的过程中,符合条件的剪拼方法有三种,需要分类讨论,分别如答图2-4所示.
| 1 |
| 2 |
| 1 |
| 2 |
(2)①由Rt△ACF∽Rt△BAO,可以求得AF的长度;若点C落在线段BD上,则有△DCF∽△DBO,根据相似比例式列方程求出t的值;
②有两种情况,需要分类讨论:当0<t≤8时,如题图1所示;当t>8时,如答图1所示.
(3)本问涉及图形的剪拼.在△CDF沿x轴左右平移的过程中,符合条件的剪拼方法有三种,需要分类讨论,分别如答图2-4所示.
解答:解:(1)由题意,易证Rt△ACF∽Rt△BAO,
∴
=
.
∵AB=2AM=2AC,
∴CF=
OA=
t.
当t=2时,CF=1.
(2)①由(1)知,Rt△ACF∽Rt△BAO,
∴
=
=
,
∴AF=
OB=2,∴FD=AF=2,.
∵点C落在线段BD上,∴△DCF∽△DBO,
∴
=
,即
=
,
解得t=2
-2或t=-2
-2(小于0,舍去)
∴当t=2
-2时,点C落在线段BD上;
②当0<t≤8时,如题图1所示:
S=
BE•CE=
(t+2)•(4-
t)=-
t2+
t+4;
当t>8时,如答图1所示:
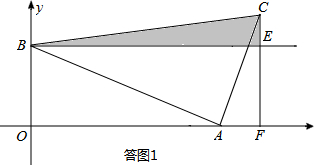
S=
BE•CE=
(t+2)•(
t-4)=
t2-
t-4.
(3)符合条件的点C的坐标为:(12,4),(8,4)或(2,4).
理由如下:
在△CDF沿x轴左右平移的过程中,符合条件的剪拼方法有三种:
方法一:如答图2所示,当F′C′=AF′时,点F′的坐标为(12,0),
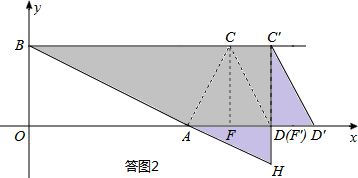
根据△C′D′F′≌△AHF′,△BC′H为拼成的三角形,此时C′的坐标为(12,4);
方法二:如答图3所示,当点F′与点A重合时,点F′的坐标为(8,0),
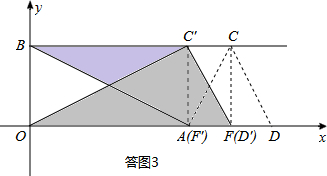
根据△OC′A≌△BAC′,可知△OC′D′为拼成的三角形,此时C′的坐标为(8,4);
方法三:当BC′=F′D′时,点F′的坐标为(2,0),
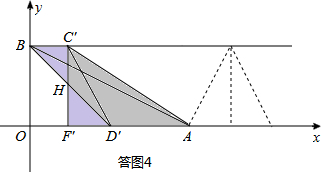
根据△BC′H≌△D′F′H,可知△AF′C′为拼成的三角形,此时C′的坐标为(2,4).
∴
| CF |
| OA |
| AC |
| AB |
∵AB=2AM=2AC,
∴CF=
| 1 |
| 2 |
| 1 |
| 2 |
当t=2时,CF=1.
(2)①由(1)知,Rt△ACF∽Rt△BAO,
∴
| AF |
| OB |
| AC |
| AB |
| 1 |
| 2 |
∴AF=
| 1 |
| 2 |
∵点C落在线段BD上,∴△DCF∽△DBO,
∴
| CF |
| OB |
| DF |
| OD |
| ||
| 4 |
| 2 |
| t+4 |
解得t=2
| 5 |
| 5 |
∴当t=2
| 5 |
②当0<t≤8时,如题图1所示:
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
当t>8时,如答图1所示:

S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
(3)符合条件的点C的坐标为:(12,4),(8,4)或(2,4).
理由如下:
在△CDF沿x轴左右平移的过程中,符合条件的剪拼方法有三种:
方法一:如答图2所示,当F′C′=AF′时,点F′的坐标为(12,0),

根据△C′D′F′≌△AHF′,△BC′H为拼成的三角形,此时C′的坐标为(12,4);
方法二:如答图3所示,当点F′与点A重合时,点F′的坐标为(8,0),

根据△OC′A≌△BAC′,可知△OC′D′为拼成的三角形,此时C′的坐标为(8,4);
方法三:当BC′=F′D′时,点F′的坐标为(2,0),

根据△BC′H≌△D′F′H,可知△AF′C′为拼成的三角形,此时C′的坐标为(2,4).
点评:本题考查了坐标平面内几何图形的多种性质,是一道难度较大的中考压轴题.涉及到的知识点包括相似三角形、全等三角形、点的坐标、几何变换(旋转、平移、对称)、图形的剪拼、解方程等,非常全面;分类讨论的思想贯穿第(2)②问和第(3)问,第(3)问还考查了几何图形的空间想象能力.本题涉及考点众多,内涵丰富,对考生的数学综合能力要求较高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
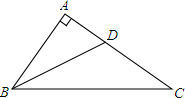 (2013•丽水)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是
(2013•丽水)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是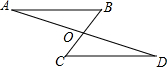 (2013•丽水)如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°,则∠C的度数是( )
(2013•丽水)如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°,则∠C的度数是( )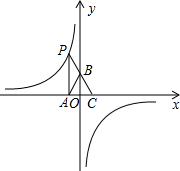 (2013•丽水)如图,点P是反比例函数y=
(2013•丽水)如图,点P是反比例函数y=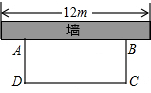 (2013•丽水)如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12 m.设AD的长为x m,DC的长为y m.
(2013•丽水)如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12 m.设AD的长为x m,DC的长为y m.