ЬтФПФкШн
ЁОЬтФПЁПГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() КЭЕу
КЭЕу![]() ЖМЪЧДг
ЖМЪЧДг![]() ЕуГіЗЂЃЌЕу
ЕуГіЗЂЃЌЕу![]() дкетИіГЄЗНаЮЕФБпЩЯЫГЪБеыдЫЖЏЃЌЕу
дкетИіГЄЗНаЮЕФБпЩЯЫГЪБеыдЫЖЏЃЌЕу![]() дкетИіГЄЗНаЮЕФБпЩЯФцЪБеыдЫЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧУПУы1ИіЕЅЮЛЃЌЩшЫќУЧЕФдЫЖЏЪБМфЪЧ
дкетИіГЄЗНаЮЕФБпЩЯФцЪБеыдЫЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧУПУы1ИіЕЅЮЛЃЌЩшЫќУЧЕФдЫЖЏЪБМфЪЧ![]() Уы
Уы![]()
ЃЈ1ЃЉ![]() ЪБЃЌЧѓЯпЖЮ
ЪБЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉдк![]() дЫЖЏЙ§ГЬжаЃЌСЌНг
дЫЖЏЙ§ГЬжаЃЌСЌНг![]() ЃЌЩшЯпЖЮ
ЃЌЩшЯпЖЮ![]() КЭЕу
КЭЕу![]() ЫљОЙ§ЕФТЗЯпЫљзщГЩЕФЗтБеЕФЭМаЮУцЛ§ЪЧ
ЫљОЙ§ЕФТЗЯпЫљзщГЩЕФЗтБеЕФЭМаЮУцЛ§ЪЧ![]() ЃЌЧѓГі
ЃЌЧѓГі![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂзЂУї
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂзЂУї![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉдкЩЯвЛЮЪжаЃЌЪЧЗёДцдкФГИіЪБПЬ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЪЧГЄЗНаЮ
ЪЧГЄЗНаЮ![]() УцЛ§ЕФвЛАыЃПШєДцдкЃЌЧѓГі
УцЛ§ЕФвЛАыЃПШєДцдкЃЌЧѓГі![]() ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉЕБ![]() Еудк
Еудк![]() ЩЯдЫЖЏЪБЃЈВЛАќРЈЕу
ЩЯдЫЖЏЪБЃЈВЛАќРЈЕу![]() ЃЉЃЌДцВЛДцдкФГвЛЪБПЬ
ЃЉЃЌДцВЛДцдкФГвЛЪБПЬ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЪЧжБНЧШ§НЧаЮТ№ЃПШєДцдкЃЌЧѓГі
ЪЧжБНЧШ§НЧаЮТ№ЃПШєДцдкЃЌЧѓГі![]() ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
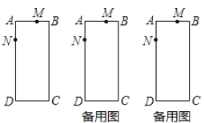
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉДцдкЃЌ
ЃЛЃЈ3ЃЉДцдкЃЌ![]() ЃЛЃЈ4ЃЉДцдкЃЌ
ЃЛЃЈ4ЃЉДцдкЃЌ![]()
ЁОНтЮіЁП
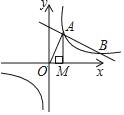
ЃЈ1ЃЉЧѓГіAMЃЌANЃЌРћгУЙДЙЩЖЈРэЧѓНтМДПЩЃЎ
ЃЈ2ЃЉЗжСНжжЧщаЮЃКЕБ0ЃМtЁм4ЪБЃЌЕБ4ЃМtЃМ10ЪБЃЌЗжБ№ЧѓНтМДПЩЃЎ
ЃЈ3ЃЉИљОнЗНГЬНтОіЮЪЬтМДПЩЃЎ
ЃЈ4ЃЉЙлВьЭМЯѓПЩжЊЃЌЁЯMANЃЌЁЯANMВЛПЩФмЪЧжБНЧЃЎЕБЁЯAMN=90ЁуЪБЃЌИљОнAN2=AM2+MN2ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
НтЃКЃЈ1ЃЉЕБt=3ЪБЃЌAM=3ЃЌAN=3ЃЌ
дкRtЁїANMжаЃЌЁпЁЯMAN=90ЁуЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ0ЃМtЁм4ЪБЃЌ![]() ЃЎ
ЃЎ
ЕБ4ЃМtЃМ10ЪБЃЌ
![]() ЃЛ
ЃЛ
Ёр![]()
ЃЈ3ЃЉЂйШєЕу![]() дк
дк![]() ЖЮЃЌМД
ЖЮЃЌМД![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЈЩсШЅЃЉЃЛ
ЃЈЩсШЅЃЉЃЛ
ЂкШєЕу![]() дк
дк![]() ЯпЖЮЃЌМД
ЯпЖЮЃЌМД![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЕБЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌЁЯMANЃЌЁЯANMВЛПЩФмЪЧжБНЧЃЎ
ЩЯдЫЖЏЪБЃЌЁЯMANЃЌЁЯANMВЛПЩФмЪЧжБНЧЃЎ
ЕБ![]() ЪБЃЌШчЭМЃКЙ§MзїMGЁЭANЃЌ
ЪБЃЌШчЭМЃКЙ§MзїMGЁЭANЃЌ
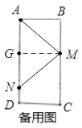
Ёр![]()
гЩЬтвтжЊЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЁрТњзуЬѕМўЕФtЕФжЕЮЊ8ЃЎ