题目内容
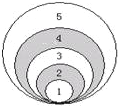
【题目】如图:同学们在操场的一个圆形区域内玩投掷沙包的游戏,圆形区域由5个过同一点且半径不同的圆组成.经过多次实验,发现沙包如果都能落在区域内时,落在2、4两个阴影内的概率分别是0.36和0.21,设最大的圆的直径是5米,则1、3、5三个区域的面积和是_____.
【答案】2.6875πm2.
【解析】
根据题意,可得大圆的面积,再由几何概率的意义,可得第2、4两个阴影的面积所占的比例,进而可得1、3、5三个区域的面积和占的比例,计算可得其面积之和.
根据题意得,最大的圆的直径是5米,则大圆的面积为6.25πm2,
又有落在2、4两个阴影内的概率分别是0.36和0.21,
则第2、4部分的面积和占总面积的0.36+0.21=0.57,即57%,
则1、3、5三个区域的面积占总面积的1-0.57=0.43,即43%,
故1、3、5三个区域的面积和为6.25π×0.43=2.6875π m2.
故答案是:2.6875π m2.

练习册系列答案
相关题目