Question

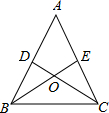如图，△ABC中，已知AB=AC，BE，CD分别是∠ABC，∠ACB的角平分线，下列结论：
（1）∠ABE=∠ACD；（2）BE=CD；（3）OC=OB；（4）CD⊥AB，BE⊥AC．
其中正确的是

1. A.
   （1）（3）（4）
2. B.
   （1）（2）（4）
3. C.
   （1）（2）（3）
4. D.
   （2）（3）（4）

Answer 1

C
分析：根据全等三角形的判定与性质，等边对等角，等角对等边和角平分线的定义即可求解．
解答：∵AB=AC，
∴∠ABC=∠ACB；
∵BE，CD分别是∠ABC，∠ACB的角平分线，
∴∠ABE=∠ACD，故（1）正确；
∴∠OBC=∠OCB，
∴OC=OB，故（3）正确；
在△DOB和△EOC中，
，
∴△DOB≌△EOC（ASA），
∴OD=OE，
∴BE=CD，故（2）正确；
无法证明CD⊥AB，BE⊥AC，故（4）错误．
故选C．
点评：本题考查全等三角形的判定与性质，等腰三角形的性质以及角平分线的定义，主要在于训练同学们的判断能力．