题目内容
 如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是
如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是α=
| β+γ |
| 2 |
α=
.| β+γ |
| 2 |
分析:先根据等腰三角形的性质及三角形内角和定理可知∠A+2∠B=180°,由α=∠BDF,β=∠CED,γ=∠AFE,△DEF是等边三角形可知∠1=120°-β,∠2=120°-γ,由三角形内角和定理可知∠A+∠1+γ=180°,∠B+α+∠2=180°,再把所得式子联立即可求出α、β、γ的关系.
解答: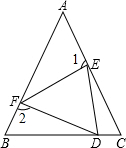 解:∵△ABC中,AB=AC,
解:∵△ABC中,AB=AC,
∴∠B=∠C,
∴∠A+2∠B=180°①,
∵△DEF是等边三角形,α=∠BDF,β=∠CED,γ=∠AFE,
∴∠1=120°-β,∠2=120°-γ,
在△AEF中,∠A+∠1+γ=180°,即∠A+120°-β+γ=180°②,
在△BDF中,∠B+α+∠2=180°,即∠B+α+120°-γ=180°③,
①②③联立,解得α=
.
故答案为:α=
.
 解:∵△ABC中,AB=AC,
解:∵△ABC中,AB=AC,∴∠B=∠C,
∴∠A+2∠B=180°①,
∵△DEF是等边三角形,α=∠BDF,β=∠CED,γ=∠AFE,
∴∠1=120°-β,∠2=120°-γ,
在△AEF中,∠A+∠1+γ=180°,即∠A+120°-β+γ=180°②,
在△BDF中,∠B+α+∠2=180°,即∠B+α+120°-γ=180°③,
①②③联立,解得α=
| β+γ |
| 2 |
故答案为:α=
| β+γ |
| 2 |
点评:本题考查的是等边三角形及等腰三角形的性质,解答此类题目时往往用到三角形的内角和是180°是解答此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图在△ABC中,已知点D、E、F分别为边BC,AD,CE的中点,且△ABC的面积是4,则△BEF的面积是
如图在△ABC中,已知点D、E、F分别为边BC,AD,CE的中点,且△ABC的面积是4,则△BEF的面积是 15、如图,△ABC中,已知AB=AC,要使AD=AE,需要添加的一个条件是
15、如图,△ABC中,已知AB=AC,要使AD=AE,需要添加的一个条件是 如图,△ABC中,已知AB=AC,BD=DC,则∠ADB=
如图,△ABC中,已知AB=AC,BD=DC,则∠ADB= 对同一图形,从不同的角度看就会有不同的发现,请根据右图解决以下问题:
对同一图形,从不同的角度看就会有不同的发现,请根据右图解决以下问题: