题目内容
【题目】如图，抛物线y=﹣x2+bx+c经过B（3，0）、C（0，3）两点，
（1）求抛物线的函数关系式；
（2）直接写出，当y≥3时，x的取值范围是_____；
（3）在抛物线的对称轴上是否存在点M点，使△MOB是等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
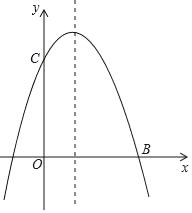
【答案】（1）y=﹣x2+2x+3；（2）0≤x≤2；（3）M（1， 
）或（1，﹣
）或（1，2
）或（1，﹣2
）．
【解析】试题分析：（1）把B、C两点坐标代入抛物线解析式，利用待定系数法可求得其解析式；
（2）由解析式可求得其对称轴，求出点C关于对称轴的对称点，再结合函数图象即可得出y≥3时，x的取值范围；
（3）可设M点坐标为（1，t），根据两点间的距离公式分别表示出BM、OM和OB的长度，再分BM=BO、OM=OB和MB=MO三种情况分别得到关于t的方程，求得t的值，则可求得M点的坐标．
试题解析：解：（1）∵抛物线y=﹣x2+bx+c经过B（3，0）、C（0，3）两点，∴
，解得： 
，∴抛物线解析式为y=﹣x2+2x+3；
（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴对称轴为x=1，∴C（0，3）关于对称轴的对称点坐标为（2，3），∴当y≥3时，x的取值范围是0≤x≤2．故答案为：0≤x≤2；
（3）由（2）可知抛物线对称轴为x=1，设M（1，t）．∵B（3，0），O（0，0），∴BM2=4+t2，OM2=1+t2，OB2=9．∵△MOB为等腰三角形，∴有BM=BO、OM=OB和MB=MO三种情况，①当BM=BO时，即4+t2=9，解得t=±
，此时M点坐标为（1， 
）或（1，﹣
）；
②当OM=OB时，即1+t2=9，解得t=±2
，此时M点坐标为（1，2
）或（1，﹣2
），③当MB=MO时，即4+t2=1+t2，无实数根．
综上所述：存在满足条件的M点，其坐标为（1， 
）或（1，﹣
）或（1，2
）或（1，﹣2
）．
