题目内容
如图,⊙O的直径AB=8,C为圆周上一点,AC=4,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E.
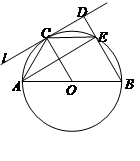
小题1:求∠AEC的度数
小题2:求证:四边形OBEC是菱形

小题1:求∠AEC的度数
小题2:求证:四边形OBEC是菱形
小题1:解:在△AOC中,AC=4,
∵ AO=OC=4,
∴ △AOC是等边三角形.………1分
∴ ∠AOC=60°,
∴∠AEC=30°.…………………3分
小题2:证明:∵OC⊥l,BD⊥l.
∴OC∥BD.……………………4分
∴ ∠ABD=∠AOC=60°.
∵ AB为⊙O的直径,
∴ △AEB为直角三角形,∠EAB=30°. …………………………7分
∴∠EAB=∠AEC.
∴ 四边形OBEC为平行四边形. …………………………………6分
又∵ OB=OC=4.
∴ 四边形OBEC是菱形. …………………………………………7 分
(1)易得△AOC是等边三角形,则∠AOC=60°,根据圆周角定理得到∠AEC=30°;
(2)根据切线的性质得到OC⊥l,则有OC∥BD,再根据直径所对的圆周角为直角得到∠AEB=90°,则∠EAB=30°,可证得AB∥CE,得到四边形OBEC为平行四边形,再由OB=OC,即可判断四边形OBEC是菱形
(2)根据切线的性质得到OC⊥l,则有OC∥BD,再根据直径所对的圆周角为直角得到∠AEB=90°,则∠EAB=30°,可证得AB∥CE,得到四边形OBEC为平行四边形,再由OB=OC,即可判断四边形OBEC是菱形

练习册系列答案
相关题目
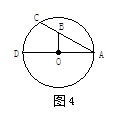
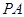 、
、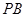 分别切⊙
分别切⊙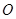 于点
于点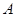 、
、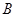 ,点
,点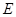 是⊙
是⊙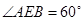 ,则
,则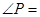 ___度.
___度.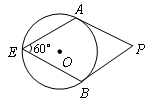
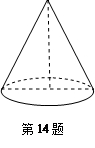
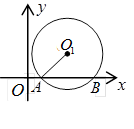
 .求⊙O1的半径.
.求⊙O1的半径.