题目内容
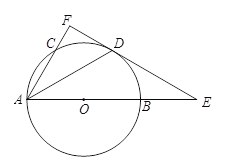
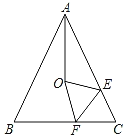
【题目】如图,在等腰△ABC中,AB=AC,把△ABC沿EF折叠,点C的对应点为O,连接AO,使AO平分∠BAC,若∠BAC=∠CFE=50°,则点O是( )
A.△ABC的内心B.△ABC的外心
C.△ABF的内心D.△ABF的外心
【答案】B
【解析】
根据等腰三角形“三线合一”的性质可得AO是BC的垂直平分线,根据垂直平分线的性质可得OB=OC,根据折叠的性质可得CF=OF,∠OFE=∠CFE=50°,进而可求出∠OAC=∠OCA=25°,可得OA=OC,即可得出O是△ABC的外心.
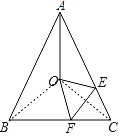
如图,连接OB、OC,
∵AB=AC,AO平分∠BAC,
∴AO是BC的垂直平分线,
∴OB=OC,
∵∠BAC=50°,AO平分∠BAC,
∴∠BAO=∠CAO=25°,
∵把△ABC沿EF折叠,点C的对应点为O,∠CFE=50°,
∴CF=OF,∠OFE=∠CFE=50°,
∴∠OFC=100°,
∴∠FCO=![]() (180°﹣100°)=40°,
(180°﹣100°)=40°,
∵AB=AC,∠BAC=50°,
∴∠ACB=![]() (180°﹣50°)=65°,
(180°﹣50°)=65°,
∴∠OCA=∠ACB﹣∠FCO=65°﹣40°=25°,
∴∠OAC=∠OCA=25°,
∴OA=OC,
∴OA=OB=OC,
∴O是△ABC的外心.
故选:B.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
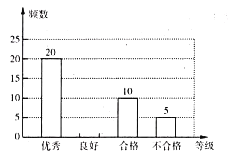
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.