��Ŀ����
����Ŀ����ͼ����֪a��b��������ABCD�ĵ�A��ֱ��a�ϣ�B��C��D������ƽ�����ƶ��仯����������״��Сʼ�ձ��ֲ��䣩������������������
��1��ͼ1������B��D��ֱ��b�ϣ���C��ֱ��b���·�����2=30�������1=������
��2��ͼ2������D��ֱ��a���Ϸ�����C��ƽ��ֱ��a��b�ڣ���B��ֱ��b���·���m��n��ʾ�ǵĶ�������д��m��n��������ϵ��˵�����ɣ�
��3��ͼ3������D��ƽ��ֱ��a��b�ڣ���B��C��ֱ��b���·���x��y��ʾ�ǵĶ�����x��y�����������ϵʽx2��2xy+y2=100����x�Ķ�����
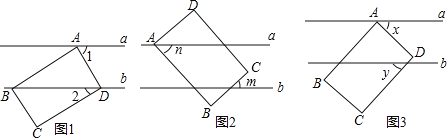
���𰸡���1��60�㣻��2��90�㣻��3��50��
����������1�����ȸ��ݽǵĺͲ��ϵ�������ADB�Ķ������ٸ���ƽ���ߵ����ʿɵá�1�Ķ�������2����C��EF��a,����a��b�ɵ�EF��a��b, �ٸ���ƽ���ߵ����ʿɵá�4+m=��BCD��n=��4�����õ��������ɵô𰸣���3����D��c��b,���������ɵ�x-y=10,�ٸ���ƽ���ߵ����ʿɵ�x+y=90������������Ͽɵô𰸣�
�⣺��1�����ı���ABCD�dz����Σ�
���ADC=90�㣬
�ߡ�2=30�㣬
���ADB=60�㣬
��a��b��
���1=��ADB=60�㣬
�ʴ�Ϊ��60�㣻
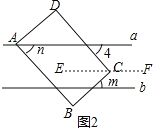
��2����ͼ2����C��EF��a��
��AB��CD��
��n=��4��
��a��b��
��EF��a��b��
���4+m=��BCD=90�㣬
��m+n=90�㣻
��3����ͼ3����D��c��b��
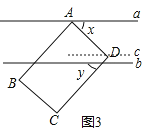
��a��b��
��a��b��c��
��x2��2xy+y2=100��
�ࣨx��y��2=100��
��x��y��
��x��y=��10����ȥ����
��x��y=10����
��a��b��
��a��b��c��
�ߡ�ADC=90�㣬
��x+y=90����
��+�ڵã�x=50�㣮
���㾦�����⿼�����ı����ۺϣ��Լ�ƽ���ߵ����ʺ��ж����ؼ���������ֱ��ƽ�У��ڴ�����ȣ�

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�