Question

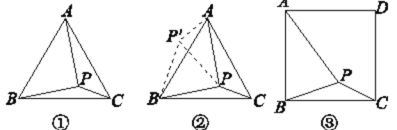
【题目】如图，四边形ABCD是正方形，E，F分别是DC和CB的延长线上的点，且BF＝DE，连接AE，AF，EF.

（1）判断△ABF与△ADE有怎样的关系，并说明理由；

（2）求∠EAF的度数,写出△ABF可以由△ADE经过怎样的图形变换得到；

（3）若BC＝6，DE＝2，求△AEF的面积．

Answer 1

【答案】（1）△ABF ≌△ADE，理由详见解析；（2）△ABF可以由△ADE绕点A顺时针方向旋转90°得到；（3）20.

【解析】

（1）利用正方形的性质结合全等三角形的判定与性质得出答案；

（2）由于△ADE≌△ABF得∠BAF=∠DAE，则∠BAF+∠BAE=90°，即∠FAE=90°，根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90度得到；

（3）首先利用勾股定理求出AE的长，由题意可得AF=AE，∠EAF=90°，再由三角形面积公式得出答案．

（1）△ABF ≌△ADE

理由如下：∵四边形ABCD是正方形，

∴AB=AD，∠ABC=∠D=90°，

∵点F是CB的延长线上的点，

∴∠ABF=90°，

在△ABF和△ADE中

∴△ABF ≌△ADE（SAS）；

（2）∵△ABF ≌△ADE

∴∠BAF=∠DAE，

∵∠DAE+∠EAB=90°，

∴∠BAF+∠EAB=90°，即∠FAE=90°，

∴△ABF可以由△ADE绕点A顺时针方向旋转90°得到；

（3）∵BC=6，

∴AD=6，

在Rt△ADE中，DE=2，AD=6，

∴AE= =

∵△ABF可以由△ADE绕点A顺时针方向旋转90 度得到，

∴AF=AE=，∠EAF=90°，

∴S△AEF=AFAE=20