题目内容
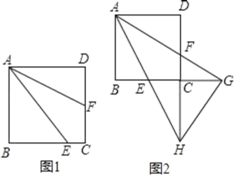
【题目】如图,正方形ABCD中,E为BC边上任意点,AF平分∠EAD,交CD于点F.
(1)如图1,若点F恰好为CD中点,求证:AE=BE+2CE;
(2)在(1)的条件下,求![]() 的值;
的值;
(3)如图2,延长AF交BC的延长线于点G,延长AE交DC的延长线于点H,连接HG,当CG=DF时,求证:HG⊥AG.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)延长BC交AF的延长线于点G,利用“AAS”证△ADF≌△GCF得AD=CG,据此知CG=BC=BE+CE,根据EG=BE+CE+CE=BE+2CE=AE即可得证;
(2)设CE=a,BE=b,则AE=2a+b,AB=a+b,在Rt△ABE中,由AB2+BE2=AE2可得b=3a,据此可得答案;
(3)连接DG,证△ADF≌△DCG得∠CDG=∠DAF,再证△AFH∽△DFG得![]() ,结合∠AFD=∠HFG,知△ADF∽△HGF,从而得出∠ADF=∠FGH,根据∠ADF=90°即可得证.
,结合∠AFD=∠HFG,知△ADF∽△HGF,从而得出∠ADF=∠FGH,根据∠ADF=90°即可得证.
解:(1)如图1,延长BC交AF的延长线于点G,
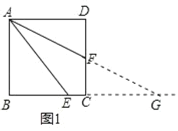
∵AD∥CG,
∴∠DAF=∠G,
又∵AF平分∠DAE,
∴∠DAF=∠EAF,
∴∠G=∠EAF,
∴EA=EG,
∵点F为CD的中点,
∴CF=DF,
又∵∠DFA=∠CFG,∠FAD=∠G,
∴△ADF≌△GCF(AAS),
∴AD=CG,
∴CG=BC=BE+CE,
∴EG=BE+CE+CE=BE=2CE=AE;
(2)设CE=a,BE=b,则AE=2a+b,AB=a+b,
在Rt△ABE中,AB2+BE2=AE2,即(a+b)2+b2=(2a+b)2,
解得b=3a,b=﹣a(舍),
∴![]() ;
;
(3)如图2,连接DG,
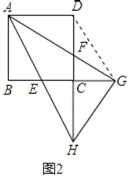
∵CG=DF,DC=DA,∠ADF=∠DCG,
∴△ADF≌△DCG(SAS),
∴∠CDG=∠DAF,
∴∠HAF=∠FDG,
又∵∠AFH=∠DFG,
∴△AFH∽△DFG,
∴![]() ,
,
又∵∠AFD=∠HFG,
∴△ADF∽△HGF,
∴∠ADF=∠FGH,
∵∠ADF=90°,
∴∠FGH=90°,
∴AG⊥GH.

【题目】某超市为了回惯顾客,计划于周年店庆当天举行抽奖活动.凡是购物金额达到m元及以上的顾客,都将获得抽奖机会.规则如下:在一个不透明袋子里装有除数字标记外其它完全相同的4个小球,数字标记分别为“a” 、“b”、“c”、“0” (其中正整数a、b、c满足a+b+c=30且a>15).顾客先随机摸出一球后不放回,再摸出第二球,则两球标记的数字之和为该顾客所获奖励金额(单位:元)、经调查发现,每日前来购物的顾客中,购物金额及人数比例如下表所示:
购物金额x (单位:元) | 0<x<100 | 100≤x<200 | 200≤x<300 | x≥300 |
人数比例 |
|
|
|
|
现预计活动当天购物人数将达到200人.
(1)在活动当天,某顾客获得抽奖机会,试用画树状图或列表的方法,求该顾客获得a元奖励金的概率;
(2)以每位抽奖顾客所获奖励金的平均数为决策依据,超市设定奖励总金额不得超过2000元,且尽可能让更多的顾客参与抽奖活动,问m应定为100元?200元?还是300元?请说明理由.