题目内容
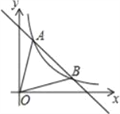
【题目】如图，一次函数y=﹣x+5的图象与反比例函数y=kx-1（k≠0）在第一象限的图象交于A（1，n）和B两点．
（1）求反比例函数的解析式与点B坐标；
（2）求△AOB的面积；
（3）在第一象限内，当一次函数y=﹣x+5的值小于反比例函数y=kx-1（k≠0）的值时，写出自变量x的取值范围．
【答案】（1）
,(4,1);(2) 
;(3)x的取值范围为0<x<1或x>4.
【解析】（1）将点A的坐标（1，4）代入，即可求出反比例函数的解析式；
（2）可求得点B的坐标，再将AB两点代入y=k1x+b，从而得出k1和b，再令y=0，求得直线和x轴的交点坐标，将三角形ABC的面积化为两个三角形的面积之差；
（3）反比例函数值大于一次函数值，即反比例函数的图象在一次函数的图象的上方时自变量的取值范围即可．
解：（1）∵一次函数y=﹣x+5的图象过点A（1，n），
∴n=﹣1+5，解得：n=4，
∴点A的坐标为（1，4）．
∵反比例函数y=
（k≠0）过点A（1，4），
∴k=1×4=4，
∴反比例函数的解析式为y=
．
联立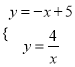
，解得： 
或
，
∴点B的坐标为（4，1）．
（2）延长AB交x轴与点C，则C（5，0），如图所示．
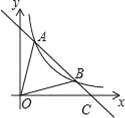
∵A（1，4），B（4，1），
∴S△AOB=S△AOC﹣S△BOC=
OCyA﹣
OCyB=10﹣
=
．
（3）观察函数图象，发现：
当0＜x＜1或x＞4时，反比例函数图象在一次函数图象上方，
∴当一次函数y=﹣x+5的值小于反比例函数y=
（k≠0）的值时，x的取值范围为0＜x＜1或x＞4．
“点睛”本题考查了反比例函数和一次函数的交点问题，以及用待定系数法求反比例函数和一次函数的解析式，是基础知识要熟练掌握．解题的关键是：（1）联立两函数解析式成二元一次方程组；（2）求出点C的坐标；（3）根据函数图象上下关系结合交点横坐标解决不等式．本题属于基础题，难度不大，解决该题型题目时，联立两函数解析式成方程组，解方程组求出交点的坐标是关键．
