题目内容
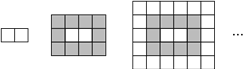
【题目】如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,

(1)按此规律,图案⑦需____根火柴棒;第n个图案需____根火柴棒.
(2)用2018根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.
【答案】(1)图案⑦需50根火柴棒;图案n需火柴棒7n+1根;(2)2017是第288个图案.理由见解析.
【解析】
(1)根据图案①、②、③中火柴棒的数量可知,第1个图形中火柴棒有8根,每多一个多边形就多7根火柴棒,由此可知第n个图案需火柴棒8+7(n-1)=7n+1根,令n=7可得答案.
(2)令8+7(n-1)=7n+1=2017求得n值即可.
解:(1)∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
∴图案n需火柴棒:8+7(n-1)=7n+1根;
当n=7时,7n+1=7×7+1=50,
∴图案⑦需50根火柴棒;
(2)令7n+1=2017,
解得n=288,
故2017是第288个图案.

练习册系列答案
相关题目