题目内容
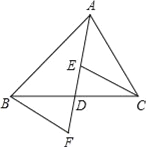
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】∵AD是△ABC的中线,
∴BD=CD,
∴△ABD的面积=△ACD的面积,
在△BDF和△CDE中,
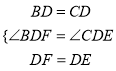 ,
,
∴△BDF≌△CDE(SAS),故①②正确
∴∠F=∠CED,∠DEC=∠F,
∴BF∥CE,故③正确,
∵∠FBD=35°,∠BDF=75°,
∴∠F=180°35°75°=70°,
∴∠DEC=70°,故④正确;
综上所述,正确的是①②③④4个。
故答案为:D.
点睛: 本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).