题目内容
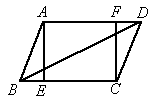
 21、如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H.
21、如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H.(1)图中的全等三角形有
2
对,它们分别是△AEG≌△CFH和△BEH≌△DFG
;(不添加任何辅助线)(2)请在(1)问中选出一对你认为全等的三角形进行证明.我选择的是:
△AEG≌△CFH
.分析:(1)全等三角形有:△AEG≌△CFH,BEH≌△DFG;
(2)利用ASA证明△AEG≌△CFH.
(2)利用ASA证明△AEG≌△CFH.
解答:解:(1)∵四边形ABCD是平行四边形ABCD,∴∠E=∠F,∠B=∠D,∠EAG=∠FCH,
∵AE=CF,∴△AEG≌△CFH和△BEH≌△DFG.
(2)如证明:△AEG≌△CFH.
∵四边形ABCD是平行四边形,
∴∠B=∠D,∠EAG=∠B,∠D=∠FCH,
∴∠EAG=∠FCH.
又∵BA∥DC,∴∠E=∠F,
又∵AE=CF,
∴△AEG≌△CFH.
∵AE=CF,∴△AEG≌△CFH和△BEH≌△DFG.
(2)如证明:△AEG≌△CFH.
∵四边形ABCD是平行四边形,
∴∠B=∠D,∠EAG=∠B,∠D=∠FCH,
∴∠EAG=∠FCH.
又∵BA∥DC,∴∠E=∠F,
又∵AE=CF,
∴△AEG≌△CFH.
点评:需注意应有规律的去找全等三角形,在证明全等的时候注意利用平行四边形的性质.

练习册系列答案
相关题目
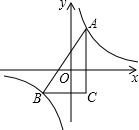 (2011•延平区质检)如图,A、B分别是函数
(2011•延平区质检)如图,A、B分别是函数
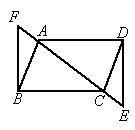
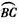 的中点,DE⊥AC平点E,DE=6cm,CE=2cm。
的中点,DE⊥AC平点E,DE=6cm,CE=2cm。