题目内容
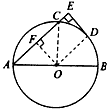
如图,AB、AC分别是⊙O的直径和弦,D为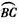 的中点,DE⊥AC平点E,DE=6cm,CE=2cm。
的中点,DE⊥AC平点E,DE=6cm,CE=2cm。
(1)求证:DE是⊙O的切线;
(2)求弦AC的长;
(3)求直径AB的长。
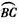 的中点,DE⊥AC平点E,DE=6cm,CE=2cm。
的中点,DE⊥AC平点E,DE=6cm,CE=2cm。(1)求证:DE是⊙O的切线;
(2)求弦AC的长;
(3)求直径AB的长。
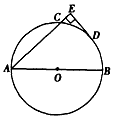
| 解:(1)证明:连接OD、OC, ∵D是 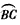 中点, 中点,∴ 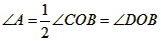 ∴AE∥OD, ∵DE⊥AE, ∴DE⊥OD, ∴DE是⊙O的切线; (2)作OF⊥AC于点F,则F为AC中点,可得矩形EFOD, ∴OF=DE=6, ∴OC=OD=FE=CF+CE=CF+2, 在Rt△COF中,由勾股定理有OF2+FC2=OC2=(FC+2)2, ∴62+FC2=FC2+4FC+4, ∴FC=8,AC=2FC=16(cm); (3)由(2)知OF2+FC2=OC2, ∴ 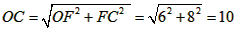 , ,∴AB=2OC=20(cm)。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 25、如图,AB、AC分别为⊙O的直径和弦,D为劣弧AC上一点,DE⊥AB于H交⊙O于E,交AC于点F,P为ED延长线上的一点.
25、如图,AB、AC分别为⊙O的直径和弦,D为劣弧AC上一点,DE⊥AB于H交⊙O于E,交AC于点F,P为ED延长线上的一点. 如图,AB、AC分别切⊙O于M、N两点,点D在⊙O上,且∠BDC=60°,则∠A=( )°.
如图,AB、AC分别切⊙O于M、N两点,点D在⊙O上,且∠BDC=60°,则∠A=( )°. 如图,AB、AC分别为⊙O的内接正六边形、内接正方形的一边,BC是圆内接n边形的一边,则n等于( )
如图,AB、AC分别为⊙O的内接正六边形、内接正方形的一边,BC是圆内接n边形的一边,则n等于( )