题目内容
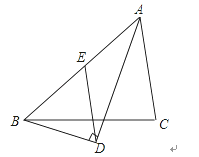
【题目】如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足_________条件时,四边形BEDF是正方形.

【答案】∠ABC=90°
【解析】分析: 由题意知,四边形DEBF是平行四边形,再通过证明一组邻边相等,可知四边形DEBF是菱形, 进而得出∠ABC=90°时,四边形BEDF是正方形.
详解: 当△ABC满足条件∠ABC=90°,四边形DEBF是正方形.
理由:∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形
∵BD是∠ABC的平分线,
∴∠EBD=∠FBD,
又∵DE∥BC,
∴∠FBD=∠EDB,则∠EBD=∠EDB,
∴BE=DE.
故平行四边形DEBF是菱形,
当∠ABC=90°时,菱形DEBF是正方形.
故答案为:∠ABC=90°.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目