题目内容
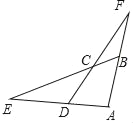
【题目】如图,点![]() 是
是![]() 三个内角的角平分线的交点,连接
三个内角的角平分线的交点,连接![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的度数为__________.
的度数为__________.

【答案】![]()
【解析】
由角平分线的性质可得∠ABP+∠BAP=60°,由“SAS”可证△ACP≌△BCP,可得AP=PE,∠CAP=∠CEP,可得PE=BE,由等腰三角形的性质和外角性质可得∠PAB=2∠PBA,即可求解.
如图,在BC上截取CE=AC,连接PE,
∵∠ACB=60°,
∴∠CAB+∠ABC=120°
∵点P是△ABC三个内角的角平分线的交点,
∴∠CAP=∠BAP=![]() ∠CAB,∠ABP=∠CBP=
∠CAB,∠ABP=∠CBP=![]() ∠ABC,∠ACP=∠BCP,
∠ABC,∠ACP=∠BCP,
∴∠ABP+∠BAP=60°
∵CA=CE,∠ACP=∠BCP,CP=CP
∴△ACP≌△ECP(SAS)
∴AP=PE,∠CAP=∠CEP
∵CA+AP=BC,且CB=CE+BE,
∴AP=BE,
∴BE=PE,
∴∠EPB=∠EBP,
∴∠PEC=∠EBP+∠EPB=2∠PBE=∠CAP
∴∠PAB=2∠PBA,且∠ABP+∠BAP=60°,
∴∠PAB=40°,
∴∠CAB=80°
故答案为:80°.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目