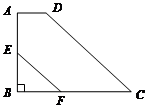题目内容
我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:如图1,在四边形ABCD中,取对角线BD的中点O,连结OA、OC. 显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.

(1)试说明直线AE是“好线”的理由;
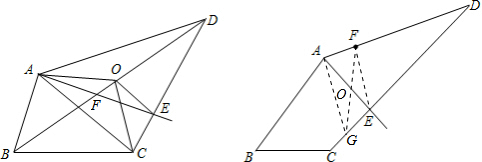
(2)如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,只需对画图步骤作适当说明(不需要说明“好线”的理由).

(1)试说明直线AE是“好线”的理由;
(2)如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,只需对画图步骤作适当说明(不需要说明“好线”的理由).
(1)∵AO是△ABD的中线,∴AO平分△ABD的面积,
同理,CO平分△CBD的面积,于是,折线AOC平分四边形ABCD的面积.
若记四边形ABCD的面积为S,有S四边形OABC=S.
∵OE∥AC,∴S△OAC=S△EAC……………………………………………… (1分)
∴S四边形EABC=S△EAC+S△ABC=S△OAC+S△ABC=S四边形OABC=S……………(2分)
∴直线AE是四边形ABCD的一条好线. ……………………………………(3分)
(2)连结EF,过点A作EF的平行线,交CD于点P,作直线PF,
则直线PF即为所要求作的好线.……………………………………(5分)
同理,CO平分△CBD的面积,于是,折线AOC平分四边形ABCD的面积.
若记四边形ABCD的面积为S,有S四边形OABC=S.
∵OE∥AC,∴S△OAC=S△EAC……………………………………………… (1分)
∴S四边形EABC=S△EAC+S△ABC=S△OAC+S△ABC=S四边形OABC=S……………(2分)
∴直线AE是四边形ABCD的一条好线. ……………………………………(3分)
(2)连结EF,过点A作EF的平行线,交CD于点P,作直线PF,
则直线PF即为所要求作的好线.……………………………………(5分)

(1)设AE与OC的交点是F.要说明直线AE是“好线”,根据已知条件中的折线AOC能平分四边形ABCD的面积,只需说明三角形AOF的面积等于三角形CEF的面积.则根据两条平行线间的距离相等,结合三角形的面积个数可以证明三角形AOE的面积等于三角形COE的面积,再根据等式的性质即可证明;
(2)根据两条平行线间的距离相等,只需借助平行线即可作出过点F的“好线”.
(2)根据两条平行线间的距离相等,只需借助平行线即可作出过点F的“好线”.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 是原点,
是原点, 三点的坐标分别
三点的坐标分别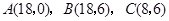 ,四边形
,四边形 是梯形,点
是梯形,点 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿 向终点
向终点 运动,速度为每秒
运动,速度为每秒 个单位,点
个单位,点 沿
沿 向终点
向终点 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动. 的解析式.
的解析式. 秒.如果点
秒.如果点 个单位,试写出点
个单位,试写出点 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出

 中,
中, ,点
,点 是边
是边 的中点, 连结
的中点, 连结 交
交 于点
于点 ,
, 的延长线于点
的延长线于点 .
.

 ,
, ,求线段
,求线段 的长
的长 和
和 . 现给出下列命题:
. 现给出下列命题:
 ,则
,则 ;②若
;②若 ,则DF=2AD.
,则DF=2AD.
 是
是 的一条角平分线,
的一条角平分线, ∥
∥ 交
交 于点
于点 ,
, ∥
∥ ,求证:四边形
,求证:四边形 是菱形(7分)
是菱形(7分)


 ( )
( ) ____________(等量代换)
____________(等量代换) 是菱形(____________________________________________)
是菱形(____________________________________________)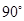 ,∠C=
,∠C=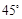 ,AD=1,BC=4,点E为AB中点,EF∥DC交BC于点F,求EF的长。
,AD=1,BC=4,点E为AB中点,EF∥DC交BC于点F,求EF的长。