��Ŀ����
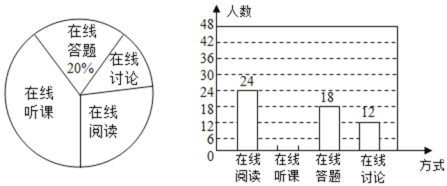
����Ŀ��Ϊ�˽�2012��ȫ����ѧ���������������о�����Ŀ��֪ʶ��Ȩ������������������˲��ֲ���ͬѧ�ijɼ�����������������ͳ��ͼ��

���������ͼ���ṩ����Ϣ������������⣺
��1������������������ ����
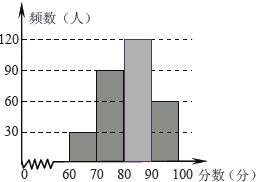
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��������ͳ��ͼ�У�m=�� ����������60��x��70��Բ�Ľ�=�� ���㣻
��4���μӱ�����С��˵�����ı����ɼ������г��ͬѧ�ɼ�����λ�����ݴ��ƶ����ijɼ������� ���������ڣ�
��5����������ɼ�80�����ϣ���80�֣�Ϊ���㣬��ô����Ƹþ�����Ŀ�������ʴ�Լ���� ����
���𰸡���1��300����2������������3��30��36����4��80��x��90����5��60%
����������������1�����õ�һ���Ƶ������Ƶ�ʼ��ɵõ�����������
��2������80��x��90��Ƶ�����ɲ�ȫֱ��ͼ��
��3��90��300��Ϊ70��x��80��Ƶ�ʣ������m��ֵ������360�����Զ�Ӧ�ı�����÷�����60��x��70��Բ�Ľǣ�
��4��������λ�����壬�ҵ�λ���м�λ�õ����������ڵ��鼴�ɣ�
��5���������ɼ�80�����ϵ���������Ƶ����Ӽ��ɵõ��Ƹþ�����Ŀ�������ʣ�
��⣺��1���˴ε������������Ϊ30��0.1=300��
��2���������Ƶ����300-30-90-50=120��
��3��70��x��80һ��İٷֱ��ǣ�![]() =0.3=30%����m=30��
=0.3=30%����m=30��
������60��x��70��Բ�Ľ���360���![]() =36����
=36����
�ʴ��ǣ�30��36��
��4����λ��Ϊ��150�����ݺ͵�151�����ݵ�ƽ����������150�����ݺ͵�151������λ��80��x��90��һ�飬����λ��λ��80��x��90��һ�飬
�ʴ��ǣ�80��x��90��
��5����80��x��90��90��x��100�������Ƶ����Ӽ��ɵõ������ʣ�������Ϊ60%��

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�