题目内容
【题目】有下列命题:
①两组对角分别相等的四边形是平行四边形;
②一组对边平行,一组对角相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形;
④一组对边平行,一条对角线被另一条对角线平分的四边形是平行四边形;
⑤一组对边相等,一组对角相等的四边形是平行四边形,
(1)上述五个命题中,是真命题的是 (填写序号)
(2)请选择一个假命题,并举反例说明.
【答案】(1)①②④;(2)见解析
【解析】
(1)根据平行线的判定定理写出真命题;
(2)根据反例证明解答即可.
(1)①一组对边平行,一组对角相等的四边形是平行四边形.故正确;
②两组对角分别相等的四边形是平行四边形.故正确;
③一组对边相等,一组对角相等的四边形不一定是平行四边形.故错误;
④一组对边平行,一条对角线被另一条对角线平分的四边形是平行四边形.故正确.
故答案是:①②④;
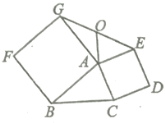
(2)③反例如下图:
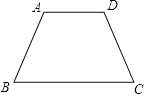
等腰梯形ABCD满足一组对边AD与BC平行,另一组对边AB与CD相等,但四边形ABCD不是平行四边形.

【题目】为宣传2022年北京﹣张家口冬季奥运会,小王在网上销售一种成本为20元/件的本届冬季奥运会宣传文化衫,销售过程中的其他各种费用(不再含文化衫成本)总计50(百元),有关销售量y(百件)与销售价格x(元/件)的相关信息如下:
销售量y(百件) | y=﹣0.1x+8 | y= |
销售价格x(元/件) | 30≤x≤60 | 60<x≤80 |
(1)求销售这种文化衫的纯利润w(百元)与销售价格x(元/件)的函数关系式;
(2)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?
【题目】台风“利奇马”给我县带来极端风雨天气,有一个水库8月9日8:00的水位为﹣0.1m(以10m为警戒线,记高于警戒线的水位为正)在以后的6个时刻测得的水位升降情况如下(记上升为正,单位:m)
时刻 | 1 | 2 | 3 | 4 | 5 | 6 |
升降 | 0.5 | ﹣0.4 | 0.6 | ﹣0.5 | 0.2 | ﹣0.8 |
(1)根据记录的数据,求第2个时刻该水库的实际水位;
(2)在这6个时刻中,该水库最高实际水位是多少?
(3)经过6次水位升降后,水库的水位超过警戒线了吗?