��Ŀ����
����Ŀ����֪���κ�����x��y�IJ��ֶ�Ӧֵ���±���
x �� ��1 0 1 2 3 ��
y �� 0 ��3 ��4 ��3 0 ��
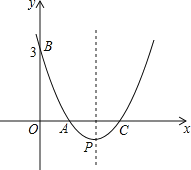
��1������κ����Ľ���ʽ��
��2����ͼ����P��ֱ��BC�·���������һ���㣬����P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC����������

��3�����������ϣ��Ƿ����һ��Q��ʹ��QBC��QC=QB����������ֱ��д��Q������꣮
���𰸡���1��y=x2��2x��3����2��P��![]() ����
����![]() ����
����![]() ����3��Q1��
����3��Q1��![]() ����
����![]() ����Q2��
����Q2��![]() ����
����![]() ����
����
��������
�����������1�����ô���ϵ����������ö��κ����Ľ���ʽ��
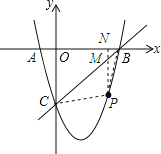
��2���������ֱ��BC�Ľ���ʽ����P��PN��x�ύֱ��BC�ڵ�M��Ȼ�����S��BPC=S��PCM+S��PMB=![]() PMON+
PMON+![]() PMNB�����ɰ�S��BPC��ʾ��P�ĺ�����x�ĺ��������ݺ�������������ֵ��
PMNB�����ɰ�S��BPC��ʾ��P�ĺ�����x�ĺ��������ݺ�������������ֵ��
��3��QC=QB����Q�����߶�BC���д�������κ����Ľ��㣬�������BC�Ľ���ʽ��Ȼ��ⷽ���鼴�ɣ�
�⣺��1����y=a��x+1����x��3���ѣ�0����3������ɵã���3=a��0+1����0��3��
��ã�a=1��y=��x+1����x��3��=x2��2x��3��
�����κ����Ľ���ʽΪ��y=x2��2x��3��
��2��S�ı���ABPC=S��ABC+S��BPC=![]() ��1��3+S��BPC��
��1��3+S��BPC��
��ֱ��BC�Ľ���ʽ��y=kx+b��
��![]() ��
��
��ã�![]() ��
��
��ֱ��BC�Ľ���ʽ�ǣ�y=x��3��
��P��PN��x�ύֱ��BC�ڵ�M����P��x��x2��2x��3����M��x��x��3��
��MP=x��3����x2��2x��3��=��x2+3x
S��BPC=S��PCM+S��PMB=![]() PMON+
PMON+![]() PMNB
PMNB
=![]() PMOB=
PMOB=![]() ����x2+3x����3=��
����x2+3x����3=��![]() x2+
x2+![]() x=��
x=��![]() ��x��
��x��![]() ��2+
��2+![]() ��0��x��3����
��0��x��3����
��x=![]() ʱ��S��BPC�����ֵΪ
ʱ��S��BPC�����ֵΪ![]() ���� S�ı���ABPC�����ֵΪ��
���� S�ı���ABPC�����ֵΪ��![]() +
+![]() =
=![]() ��
��
��ʱP��![]() ����
����![]() ����
����
��3��BC���е������ǣ�![]() ����
����![]() ����
����
���߶�BC���д��ߵĽ���ʽ��y=��x+c����![]() +c=��
+c=��![]() ��
��
���c=0��
��BC���д��ߵĽ���ʽ��y=��x��
��������ã�![]() ��
��
��ã�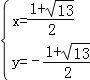 ��
�� ��
��
��Q�������ǣ�Q1��![]() ����
����![]() ����Q2��
����Q2��![]() ����
����![]() ����
����

 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д�