题目内容
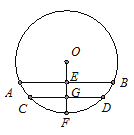
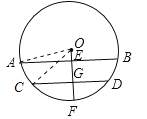
【题目】如图，圆柱形水管内原有积水的水平面宽CD=20cm，水深GF=2cm．若水面上升2cm（EG=2cm），则此时水面宽
AB为多少？
【答案】
cm．
【解析】试题分析：连接OA、OC．设⊙O的半径是R，则OG=R﹣2，OE=R﹣4．根据垂径定理，得CG=10．在直角三角形OCG中，根据勾股定理求得R的值，再进一步在直角三角形OAE中，根据勾股定理求得AE的长，从而再根据垂径定理即可求得AB的长．
试题解析：解：如图所示，连接OA、OC．
设⊙O的半径是R，则OG=R﹣2，OE=R﹣4．
∵OF⊥CD，∴CG=
CD=10cm．
在直角三角形COG中，根据勾股定理，得
R2=102+（R﹣2）2，解，得R=26．
在直角三角形AOE中，根据勾股定理，得
AE=
=
cm．
根据垂径定理，得AB=（cm）．
练习册系列答案
阅读快车系列答案
相关题目
