题目内容
【题目】如图,四条直线l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=﹣
x,l3:y3=﹣![]() x,l4:y4=﹣
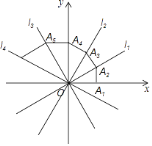
x,l4:y4=﹣![]() x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为________.
x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为________.
【答案】((![]() )2016,0)
)2016,0)
【解析】
先利用各直线的解析式得到x轴、l1、l2、y轴、l3、l4依次相交为30的角,各点的位置是每12个一循环,由于2017=168×12+1,则可判定点A2017在x轴的正半轴上,再规律得到OA2016=(![]() )2015,然后表示出点A2017坐标.
)2015,然后表示出点A2017坐标.
解:∵l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=-
x,l3:y3=-![]() x,l4:y4=-﹣
x,l4:y4=-﹣![]() x,
x,
∴x轴、l1、l2、y轴、l3、l4依次相交为30的角,
∵2017=168×12+1,
∴点A2017在x轴的正半轴上,
∵OA2=![]() =
=![]() ,
,
OA3=(![]() )2,
)2,
OA4=(![]() )3,
)3,
…
OA2017=(![]() )2016,
)2016,
∴点A2017坐标为((![]() )2016,0).
)2016,0).
故答案为((![]() )2016,0).
)2016,0).

练习册系列答案
相关题目