ΧβΡΩΡΎ»ί
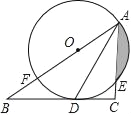
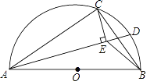
ΓΨΧβΡΩΓΩ‘ΎΆΦ1ΒΫΆΦ3÷–Θ§ΒψO «’ΐΖΫ–ΈABCDΕ‘Ϋ«œΏACΒΡ÷–ΒψΘ§ΓςMPNΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœMPNΘΫ90ΓψΘ°’ΐΖΫ–ΈABCD±Θ≥÷≤ΜΕ·Θ§ΓςMPN―Ί…δœΏACœρ”“ΤΫ“ΤΘ§ΤΫ“ΤΙΐ≥Χ÷–PΒψ Φ÷’‘Ύ…δœΏAC…œΘ§«“±Θ≥÷PM¥Ι÷±”Ύ÷±œΏAB”ΎΒψEΘ§PN¥Ι÷±”Ύ÷±œΏBC”ΎΒψFΘ°
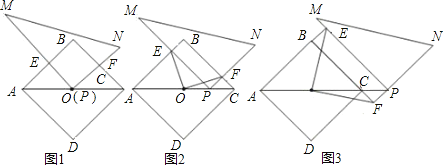
Θ®1Θ©»γΆΦ1Θ§Β±ΒψP”κΒψO÷ΊΚœ ±Θ§–¥≥ωOE”κOFΒΡ ΐΝΩΙΊœΒΘΜ
Θ®2Θ©»γΆΦ2Θ§Β±P‘ΎœΏΕΈOC…œ ±Θ§≤¬œκOE”κOF”–‘θ―υΒΡ ΐΝΩΙΊœΒ”κΈΜ÷ΟΙΊœΒΘΩ≤ΔΕ‘ΡψΒΡ≤¬œκΫαΙϊΗχ”η÷ΛΟςΘΜ
Θ®3Θ©»γΆΦ3Θ§Β±ΒψP‘ΎACΒΡ―”≥ΛœΏ…œ ±Θ§–¥≥ωOE”κOFΒΡ ΐΝΩΙΊœΒΘΜΈΜ÷ΟΙΊœΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©OEΘΫOFΘ§OEΓΆOFΘ§ΦϊΫβΈωΘΜΘ®3Θ©OEΘΫOFΘ®œύΒ»Θ©Θ§OEΓΆOFΘ®¥Ι÷±Θ©Θ°άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίάϊ”Ο’ΐΖΫ–ΈΒΡ–‘÷ ΒΟ≥ωΓœBACΘΫΓœBCAΓΔAOΘΫCOΘ§‘ΌΗυΨί“―÷ΣΒΟ≥ωΓœAEOΘΫΓœAFO=90![]() Θ§¥”ΕχΒΟΒΫΓςAEOΓ’ΓςCFOΦ¥Ω…ΘΜ
Θ§¥”ΕχΒΟΒΫΓςAEOΓ’ΓςCFOΦ¥Ω…ΘΜ
Θ®2Θ©Β±P‘ΎœΏΕΈOC…œ ±Θ§ΗυΨί’ΐΖΫ–ΈΒΟ–‘÷ œ»÷ΛΟςPFΘΫFCΘ§‘Ό÷ΛΟςΥΡ±Ώ–ΈBEPFΈΣΨΊ–ΈΘ§ΒΟΒΫBEΘΫPFΘ§¥”ΕχΒΟΒΫBEΘΫFCΘ§‘Ό÷ΛΟςΓςOBEΓ’ΓςOCFΦ¥Ω…ΘΜ
Θ®3Θ©Β±ΒψP‘ΎACΒΡ―”≥ΛœΏ…œ ±Θ§”–œύΆ§ΒΡΙΊœΒΘ§Τδ÷ΛΟςΖΫΖ®”κΘ®2Θ©άύΥΤΘ°
Θ®1Θ©ΫβΘΚ”…Χβ“βΒΟΘΚ
ΓœBACΘΫΓœBCAΘΫ45ΓψΘ§AOΘΫCOΘ§
ΓœAEOΘΫΓœAFOΘ§
‘ΎΓςAEOΚΆΓςCFO÷–
 Θ§
Θ§
ΓύΓςAEOΓ’ΓςCFOΘ®AASΘ©
ΓύOEΘΫOFΘΜ
Θ®2Θ©ΫβΘΚOEΘΫOFΘ§OEΓΆOFΘΜ
÷ΛΟςΘΚΝ§Ϋ”BOΘ§
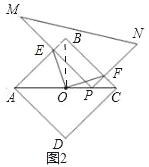
ΓΏ‘Ύ’ΐΖΫ–ΈABCD÷–Θ§OΈΣAC÷–ΒψΘ§
ΓύBOΘΫCOΘ§BOΓΆACΘ§ΓœBCAΘΫΓœABOΘΫ45ΓψΘ§
ΓΏPFΓΆBCΘ§ΓœBCOΘΫ45ΓψΘ§
ΓύΓœFPCΘΫ45ΓψΘ§PFΘΫFCΘ°
ΓΏ’ΐΖΫ–ΈABCDΘ§ΓœABCΘΫ90ΓψΘ§
ÿPFâBCȧPEâABȧ
ΓύΓœPEBΘΫΓœPFBΘΫ90ΓψΘ°
ΓύΥΡ±Ώ–ΈPEBF «ΨΊ–ΈΘ§
ΓύBEΘΫPFΘ°
ΓύBEΘΫFCΘ°
ΓύΓςOBEΓ’ΓςOCFΘ§
ΓύOEΘΫOFΘ§ΓœBOEΘΫΓœCOFΘ§
ΓΏΓœCOF+ΓœBOFΘΫ90ΓψΘ§
ΓύΓœBOE+ΓœBOFΘΫ90ΓψΘ§
ΓύΓœEOFΘΫ90ΓψΘ°
ΓύOEΓΆOFΘ°
Θ®3Θ©OEΘΫOFΘ®œύΒ»Θ©Θ§OEΓΆOFΘ®¥Ι÷±Θ©Θ°
άμ”…ΘΚΝ§Ϋ”BOΘ§
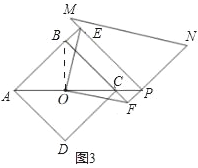
ΓΏ‘Ύ’ΐΖΫ–ΈABCD÷–Θ§OΈΣAC÷–ΒψΘ§
ΓύBOΘΫCOΘ§BOΓΆACΘ§ΓœBCAΘΫΓœABOΘΫ45ΓψΘ§
ΓύΓœOCFΘΫΓœOBE
ΓΏPFΓΆBCΘ§ΓœBCOΘΫ45ΓψΘ§
ΓύΓœFPCΘΫ45ΓψΘ§PFΘΫFCΘ°
ΓΏ’ΐΖΫ–ΈABCDΘ§ΓœABCΘΫ90ΓψΘ§
ÿPFâBCȧPEâABȧ
ΓύΓœPEBΘΫΓœPFBΘΫ90ΓψΘ°
ΓύΥΡ±Ώ–ΈPEBF «ΨΊ–ΈΘ§
ΓύBEΘΫPFΘ°
ΓύBEΘΫFCΘ°
ΓύΓςOBEΓ’ΓςOCFΘ§
ΓύOEΘΫOFΘ§ΓœBOEΘΫΓœCOFΘ§
ΓΏΓœCOF+ΓœBOFΘΫ90ΓψΘ§
ΓύΓœBOE+ΓœBOFΘΫ90ΓψΘ§
ΓύΓœEOFΘΫ90ΓψΘ°
ΓύOEΓΆOFΘ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ