题目内容
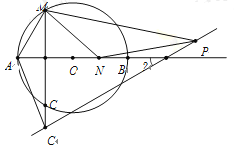
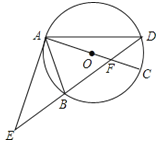
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、AE=4![]()
【解析】
试题分析:(1)、连接CD,根据直径所对的圆周角为直角得出∠ADB+∠EDC=90°,根据同弧所对的圆周角相等得出∠BAC=∠EDC,然后结合已知条件得出∠EAB+∠BAC=90°,从而说明切线;(2)、连接BC,根据直径的性质得出∠ABC=90°,根据B是EF的中点得出AB=EF,即∠BAC=∠AFE,则得出三角形相似;(3)、根据三角形相似得出![]() ,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入
,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入![]() 求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
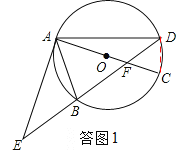
试题解析:(1)、如答图1,连接CD, ∵AC是⊙O的直径,∴∠ADC=90°. ∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB, ∴∠BAC=∠EAB+∠BAC=90°. ∴EA是⊙O的切线.
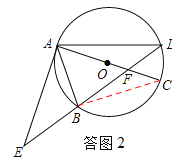
(2)、如答图2,连接BC, ∵AC是⊙O的直径,∴∠ABC=90°. ∴∠CBA=∠ABC=90°.
∵B是EF的中点,∴在Rt△EAF中,AB=BF. ∴∠BAC=∠AFE. ∴△EAF∽△CBA.
(3)、∵△EAF∽△CBA,∴![]() . ∵AF=4,CF=2, ∴AC=6,EF=2AB.
. ∵AF=4,CF=2, ∴AC=6,EF=2AB.
∴![]() ,解得AB=2
,解得AB=2![]() .∴EF=4
.∴EF=4![]() .
.
∴AE=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目