题目内容
 如图,已知正方形ABCD的边长为
如图,已知正方形ABCD的边长为| 2 |
考点:正方形的性质,角平分线的性质
专题:几何图形问题
分析:过E作EF⊥DC于F,根据正方形的性质和角平分线的性质以及勾股定理即可求出DE的长.
解答:解:过E作EF⊥DC于F,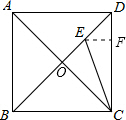
∵四边形ABCD是正方形,
∴AC⊥BD,
∵CE平分∠ACD交BD于点E,
∴EO=EF,
∵正方形ABCD的边长为
,
∴AC=
=2,
∴CO=
AC=1,
∴CF=CO=1,
∴EF=DF=DC-CF=
-1,
∴DE=
=
=2-
.
故答案为:2-
.

∵四边形ABCD是正方形,
∴AC⊥BD,
∵CE平分∠ACD交BD于点E,
∴EO=EF,
∵正方形ABCD的边长为
| 2 |
∴AC=
| 2+2 |
∴CO=
| 1 |
| 2 |
∴CF=CO=1,
∴EF=DF=DC-CF=
| 2 |
∴DE=
| DF2+EF2 |
(
|
| 2 |
故答案为:2-
| 2 |
点评:本题考查了正方形的性质:对角线相等,互相垂直平分,并且每条对角线平分一组对角、角平分线的性质:角的平分线上的点到角的两边的距离相等以及勾股定理的运用.

练习册系列答案
相关题目
 如图,现有一张正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点C落在P处,点B落在O处,OP交AB于Q,折痕为MN,连接CP.
如图,现有一张正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点C落在P处,点B落在O处,OP交AB于Q,折痕为MN,连接CP.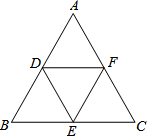 如图,已知D、E、F分别为△ABC的中点,则四边形DECF为
如图,已知D、E、F分别为△ABC的中点,则四边形DECF为