题目内容
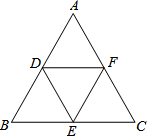 如图,已知D、E、F分别为△ABC的中点,则四边形DECF为
如图,已知D、E、F分别为△ABC的中点,则四边形DECF为考点:三角形中位线定理
专题:计算题
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得DF∥BC且DF=
BC,再根据线段中点的定义可得EC=
BC,然后根据一组对边平行且相等的四边形是平行四边形解答;根据三角形中位线定理可得△DFE周长等于△ABC的周长的一半列式计算即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵D、F分别为△ABC的中点,
∴DF∥BC且DF=
BC,
∵E是BC边的中点,
∴EC=
BC,
∴DF=EC,
∴四边形DECF为平行四边形;
∵△ABC周长为10cm,
∴△DFE周长为5cm.
故答案为:平行四边,5.
∴DF∥BC且DF=
| 1 |
| 2 |
∵E是BC边的中点,
∴EC=
| 1 |
| 2 |
∴DF=EC,
∴四边形DECF为平行四边形;
∵△ABC周长为10cm,
∴△DFE周长为5cm.
故答案为:平行四边,5.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,熟记定理以及平行四边形的判定方法是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
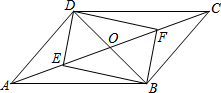 如图,平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动.
如图,平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动. 如图,已知正方形ABCD的边长为
如图,已知正方形ABCD的边长为