题目内容
九(1)班数学课题学习小组,为了研究学习二次函数问题,他们经历了实践--应用--探究的过程:
(1)实践:他们对一条公路上横截面为拋物线的单向双车道的隧道(如图①)进行测量,测得一隧道的路面宽为10m,隧道顶部最高处距地面6.25m,并画出了隧道截面图,建立了如图②所示的直角坐标系,请你求出抛物线的解析式.
(2)应用:按规定机动车辆通过隧道时,车顶部与隧道顶部在竖直方向上的高度差至少为0.5m.为了确保安全,问该隧道能否让最宽3m,最高3.5m的两辆厢式货车居中并列行驶(两车并列行驶时不考虑两车间的空隙)?
(3)探究:该课题学习小组为进一步探索抛物线的有关知识,他们借助上述拋物线模型,提出了以下两个问题,请予解答:
I.如图③,在抛物线内作矩形ABCD,使顶点C、D落在拋物线上,顶点A、B落在x轴 上.设矩形ABCD的周长为l求l的最大值.
II•如图④,过原点作一条y=x的直线OM,交抛物线于点M,交抛物线对称轴于点N,P 为直线0M上一动点,过P点作x轴的垂线交抛物线于点Q.问在直线OM上是否存在点P,使以P、N、Q为顶点的三角形是等腰直角三角形?若存在,请求出P点的坐标;若不存在,请说明理由.
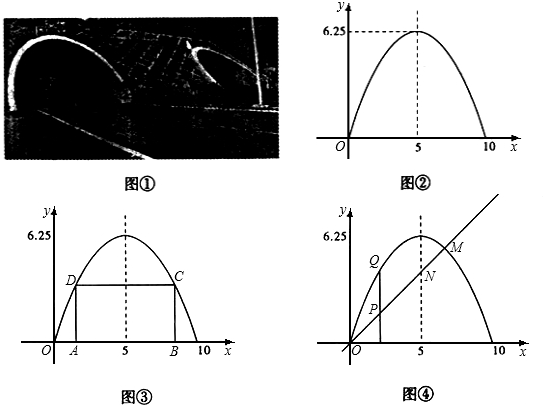
解:(1)根据坐标系可知此函数顶点坐标为(5,6.25),且图象过(10,0)点,
代入顶点式得:
y=a(x-5)2+6.25,
∴0=a(10-5)2+6.25,
解得:a=-0.25,
∴y=-0.25(x-5)2+6.25;
(2)当最宽3m,最高3.5m的两辆厢式货车居中并列行驶时,
∴10-3×2=4,
4÷2=2,
∴x=2代入解析式得:
y=-0.25(2-5)2+6.25;
y=4,
4-3.5=0.5,
∴隧道能让最宽3m,最高3.5m的两辆厢式货车居中并列行驶;
(3)I.假设AO=x,可得AB=10-2x,
∴AD=-0.25(x-5)2+6.25;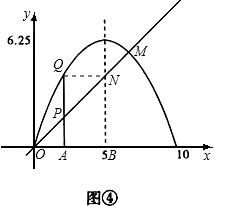
∴矩形ABCD的周长为l为:l=2[-0.25(x-5)2+6.25]+2(10-2x)=-0.5x2+x+20,
∴l的最大值为: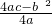 =
=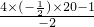 =20.5.
=20.5.
II•当以P、N、Q为顶点的三角形是等腰直角三角形,
∵P在y=x的图象上,过P点作x轴的垂线交抛物线于点Q.
∴∠POA=∠OPA=45°,
∴Q点的纵坐标为5,
∴5=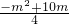 ,
,
解得:m=5± ,
,
当∠P3NQ3=90°时,过点Q3作Q3K1⊥对称轴,
当△NQ3K1为等腰直角三角形时,△NP3Q3为等腰直角三角形,
Q点在OM的上方时,P3Q3=2Q3K1,P3Q3=-
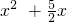 -x,
-x,
Q3K1=5-x,
Q点在OM的下方时,P4Q4=2Q4K2,P4Q4=x-(-
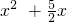 ),
),
Q4K2=x-5,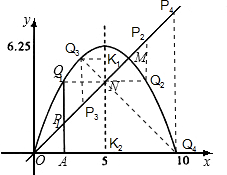
∴ x2-
x2- x+10=0,
x+10=0,
解得:x1=4,x2=10,
P3(4,4),P4(10,10)
∴使以P、N、Q为顶点的三角形是等腰直角三角形,P点的坐标为:
(5- ,5-
,5- )或(5+
)或(5+ ,5+
,5+ )或(4,4)或(10,10).
)或(4,4)或(10,10).
分析:(1)利用顶点式求出二次函数解析式即可;
(2)根据已知得出当x=2时,正好是汽车宽度,求出即可;
(3)I.首先表示出矩形周长,再利用二次函数最值公式求出;
II•利用等腰直角三角形的性质得出QN=AB=AO,以及P在y=x的图象上,即可得出P点的坐标.
点评:此题主要考查了顶点式求二次函数解析式以及二次函数最值求法和等腰直角三角形的性质,根据函数图象获取正确点的坐标以及利用y=x图象上点的性质是解决问题的关键.
代入顶点式得:
y=a(x-5)2+6.25,
∴0=a(10-5)2+6.25,
解得:a=-0.25,
∴y=-0.25(x-5)2+6.25;
(2)当最宽3m,最高3.5m的两辆厢式货车居中并列行驶时,
∴10-3×2=4,
4÷2=2,
∴x=2代入解析式得:
y=-0.25(2-5)2+6.25;
y=4,
4-3.5=0.5,
∴隧道能让最宽3m,最高3.5m的两辆厢式货车居中并列行驶;
(3)I.假设AO=x,可得AB=10-2x,
∴AD=-0.25(x-5)2+6.25;

∴矩形ABCD的周长为l为:l=2[-0.25(x-5)2+6.25]+2(10-2x)=-0.5x2+x+20,
∴l的最大值为:
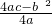 =
=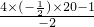 =20.5.
=20.5.II•当以P、N、Q为顶点的三角形是等腰直角三角形,
∵P在y=x的图象上,过P点作x轴的垂线交抛物线于点Q.
∴∠POA=∠OPA=45°,
∴Q点的纵坐标为5,
∴5=
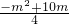 ,
,解得:m=5±
 ,
,当∠P3NQ3=90°时,过点Q3作Q3K1⊥对称轴,
当△NQ3K1为等腰直角三角形时,△NP3Q3为等腰直角三角形,
Q点在OM的上方时,P3Q3=2Q3K1,P3Q3=-

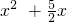 -x,
-x,Q3K1=5-x,
Q点在OM的下方时,P4Q4=2Q4K2,P4Q4=x-(-

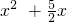 ),
),Q4K2=x-5,

∴
 x2-
x2- x+10=0,
x+10=0,解得:x1=4,x2=10,
P3(4,4),P4(10,10)
∴使以P、N、Q为顶点的三角形是等腰直角三角形,P点的坐标为:
(5-
 ,5-
,5- )或(5+
)或(5+ ,5+
,5+ )或(4,4)或(10,10).
)或(4,4)或(10,10).分析:(1)利用顶点式求出二次函数解析式即可;
(2)根据已知得出当x=2时,正好是汽车宽度,求出即可;
(3)I.首先表示出矩形周长,再利用二次函数最值公式求出;
II•利用等腰直角三角形的性质得出QN=AB=AO,以及P在y=x的图象上,即可得出P点的坐标.
点评:此题主要考查了顶点式求二次函数解析式以及二次函数最值求法和等腰直角三角形的性质,根据函数图象获取正确点的坐标以及利用y=x图象上点的性质是解决问题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
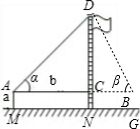
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题---测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
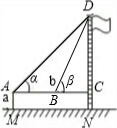 |
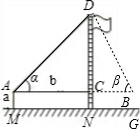 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: | 解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
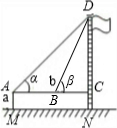 |
 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: |
解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组 活动地点:学校操场
活动时间:××××年××月××日年上午9:00 活动小组组长:×××
数学活动报告
活动小组:第一组 活动地点:学校操场
活动时间:××××年××月××日年上午9:00 活动小组组长:×××
| 课题 | 测量校内旗杆高度 |
| 目的 | 运用所学数学知识及数学方法解决实际问题--测量旗杆高度 |
| 示意图 | 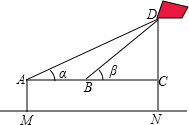 |
| 测量工具 | 皮尺、测角仪 |
| 测量数据: | AM=1.5m,AB=10m,∠α=30°,∠β=60° |
| 计算过程(结 果保留根号) |
解: |
| 测量结果 | DN= |
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |  |  | |
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
| 计算过程(结 果保留根号) | 解: | 解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题---测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 | 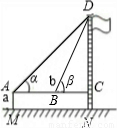 | 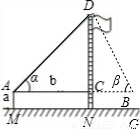 | |
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
| 计算过程(结 果保留根号) | 解: | 解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)