题目内容
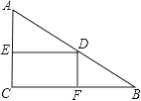
【题目】在Rt△ABC中,∠C=90°,AC=3,BC=4,D是AB上一动点（不与A、B重合）,DE⊥AC于点E,DF⊥BC于点F,点D由A向B移动时,矩形DECF的周长变化情况是（ ）
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大
【答案】A
【解析】试题分析：设DE=λ，运用相似三角形的性质，将矩形DECF的周长表示为λ的一次函数的形式，运用函数的性质即可解决问题．
解：设DE=λ，DF=μ；
∵DE⊥AC于点E，DF⊥BC于点F，
∴四边形DECF为矩形，
∴CF=DE=λ，CE=DF=μ，
∴矩形DECF的周长η=2λ+2μ；
∵DE∥BC，
∴△ADE∽△ABC，
∴
①；同理可证
②，
由①+②得：
，
∴μ=8﹣
∴η=2λ+16﹣
=
+16，
∵
＜0，
∴η随λ的增大而减小；
∵点D从靠近点A的某一点向点B移动时，λ逐渐变大，
∴矩形DECF的周长η逐渐减小．
故选A．
仁爱英语同步练习册系列答案
学习实践园地系列答案【题目】杭州市甲、乙两个有名的学校乐团，决定向某服装厂购买同样的演出服．如表是服装厂给出的演出服装的价格表：
购买服装的套数 | 1～39套（含39套） | 40～69套（含69套） | 70套及以上 |
每套服装的价格 | 80元 | 70元 | 60元 |
经调查：两个乐团共85人（甲乐团人数不少于46人），如果分别各自购买演出服，两个乐团共需花费6500元．请回答以下问题：
（1）如果甲、乙两个乐团联合起来购买服装，那么比各自购买服装最多可以节省多少元？
（2）甲、乙两个乐团各有多少名学生？
（3）现从甲乐团抽调a人，从乙乐团抽调b人（要求从每个乐团抽调的人数不少于5人），去儿童福利院献爱心演出，并在演出后每位乐团成员向儿童们进行“心连心活动”；甲乐团每位成员负责5位小朋友，乙乐团每位成员负责3位小朋友．这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖．请写出所有的抽调方案，并说明理由．
